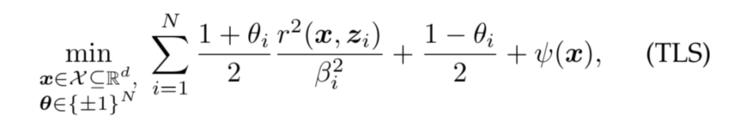來源:雷鋒網(wǎng)
上個月,我們報道了 MIT 在讀中國博士生、清華大學(xué)機械工程系校友楊珩開發(fā)用于提高自動駕駛安全性的可認證感知算法一文,引起了部分讀者的關(guān)注。然而,當(dāng)時的報道較簡略,因此 AI 科技評論親自聯(lián)系了楊珩本人,圍繞「可認證感知算法」這一較為陌生的概念再次進行了補充交流。
那么,什么叫做「可認證感知算法」(Certifiable Perception Algorithm)?它對自動駕駛,或其他機器人(Robotics)方向的研究意義是什么?它的研究難點又是什么?
事實上,「可認證感知算法」最早是一個數(shù)學(xué)上的概念,在 2016 年由蘇黎世聯(lián)邦理工學(xué)院(ETH)數(shù)學(xué)系的教授、2018 年斯隆研究獎獲得者 Afonso S. Bandeira 在 "A Note on Probably Certifiably Correct Algorithms" 一文中提出。
針對許多優(yōu)化問題在獲得一個解時、沒有后驗(a posteriori)證明該解是否為最優(yōu)解的情況,Bandeira 提出了一個 PCC(Probably Correct Certifiable)算法,不僅可以解決經(jīng)典的優(yōu)化實例問題,還可以提供一個「后驗證書」(a posteriori certificate),向研究人員證明該解為最優(yōu)解。
在 Bandeira 的這篇工作中,PCC 算法也被應(yīng)用于機器學(xué)習(xí)的某些場景,比如學(xué)習(xí)隨機塊模型(stochastic block model)。本質(zhì)上,"certificate" 是一個數(shù)學(xué)測度,揭示了研究人員求得的解與全局最優(yōu)解之間的差距。例如,當(dāng)差距非常小,只有一億分之一時,那么研究人員就能知道,該解已是近似最優(yōu),可以視為全局最優(yōu)。
受此啟發(fā),楊珩從 2018 年開始研究可認證感知算法,如今已取得一系列成果。
1. 什么是可認證算法?
在自動駕駛中,可認證感知算法存在的核心意義,是提高車輛在駕駛過程中的安全性,防止意外事故的發(fā)生。
如下圖所示,自動駕駛車輛 A(即 "robot",機器人)在路上行駛的過程中,如 " 看 " 到一輛車 B,用攝像頭拍攝一張照片,照片中會包含該車輛 B。我們假設(shè)車輛 A 的內(nèi)存里有 B 的 3D 模型,而車輛 A 的任務(wù)是估測 B 的位置和姿態(tài)(6D pose, 3D rotation and translation)。這時,A 會用一個神經(jīng)網(wǎng)絡(luò)檢測出所攝 2D 平面圖像上的所有關(guān)鍵點(keypoints),如車輪、車燈、鏡子等等,然后將這些所識別出的目標(biāo)與 3D 模型上的關(guān)鍵點進行數(shù)據(jù)關(guān)聯(lián)(data association),識別物體是車鏡、車燈或其他元件。

如果神經(jīng)網(wǎng)絡(luò)所檢測出的關(guān)鍵點與數(shù)據(jù)關(guān)聯(lián)都是正確的,那么自動駕駛的視覺感知挑戰(zhàn)(比如估測車輛 B 的位置和姿態(tài))在轉(zhuǎn)為數(shù)學(xué)優(yōu)化問題時則相對好解。但在實踐中,神經(jīng)網(wǎng)絡(luò)往往會出錯。神經(jīng)網(wǎng)絡(luò)的前端可能會輸出錯誤的關(guān)鍵點,比如,有可能將檢測出來的鏡子識別為汽車的輪子,從而建立一些不正確的關(guān)聯(lián),也就是所謂的「異常值」(outliers,上圖的紅色連線)。
在這種情況下,我們往往難以區(qū)分 2D 平面圖像與 3D 汽車模型中的對應(yīng)關(guān)系中,哪些是正確數(shù)據(jù)(inliers)、哪些是異常數(shù)據(jù)(outliers)。這時,自動駕駛車輛 A 在估測車輛 B 的姿態(tài)時,如果估計正確,那么線框圖會對應(yīng)地重疊在 A 所拍攝的 2D 圖像上;若估計錯誤,則 2D 圖像上會出現(xiàn)許多紅點(如上圖最右上角所示)。
一旦估計出錯,自動駕駛車輛則可能發(fā)生碰撞等安全事故問題。比方說,自動駕駛車輛 A 感知到同時行駛在一條馬路上的車輛 B 的存在。B 距離 A 實際只有 3 米,但如果估計錯誤,判斷 B 距離 A 有 10 米,那么 A 可能就會加速行駛,造成嚴重的事故。
所以,用于估計車輛姿態(tài)的算法不僅要告訴研究人員一個正確的結(jié)果,還要解釋這個結(jié)果有多么地正確(即解與最優(yōu)解之間的距離)。當(dāng)算法失敗時,算法也應(yīng)向駕駛自動車輛的人(或者系統(tǒng))傳遞一個信號,使駕駛員能采取其他的行動,比如接管方向盤、停車或及時尋求他人支援等。這,也是「可認證感知算法」的具體內(nèi)涵。因此,在「安全第一」的自動駕駛領(lǐng)域,可認證感知算法具有深遠的現(xiàn)實意義。
但話說回來,「可認證算法」所扮演的角色雖然聽起來很簡單,研究起來卻并不容易,因為在這個研究的過程中涉及到了對截斷最小二乘法(Truncated Least Squares, TLS)的求解。TLS 是一個非凸優(yōu)化問題,其可行域集合可能存在局部最優(yōu)點,但求解全局最優(yōu)的難度相當(dāng)于 NP 難題。
因此,盡管早期歐洲有些學(xué)校也沿著可認證算法的方向研究,但他們解決問題的切入點只停留在建模階段,且面向的場景為沒有異常值的情況。
基于 Bandeira 的工作,楊珩與他的博士導(dǎo)師 Luca Carlone 還就「可認證算法」制定了更高的標(biāo)準(zhǔn)。
假設(shè)算法為 A,A 的目標(biāo)是解決優(yōu)化問題 P,而優(yōu)化問題取決于輸入數(shù)據(jù) D。那么,如果該算法是可認證的,則必須同時滿足三個條件:
1)A 必須是多項式算法(polynomial algorithm),理論上必須要快;
2)在解決 P 后,A 要么得到一個全局最優(yōu)解,以及證明該解為全局最優(yōu)的 " 證書 "(certificate);要么失敗,沒有得到全局最優(yōu)解,只得到所謂的 "measurable suboptimality",即所求得的解與全局最優(yōu)解之間的距離;
3)對于大部分 D,A 都能將 P 解到全局最優(yōu)。
第三個條件由楊珩與 Luca Carlone 添加,目的是為了排除近似算法。所謂 " 近似算法 "(approximate algorithm),指的是算法得到的解永遠只能是近似最優(yōu)。在自動駕駛中,近似算法相當(dāng)于在任何情況下都無法取得全局最優(yōu)解,一直 " 報錯 ",這會對駕駛安全造成極大隱患。
所以,在楊珩與團隊的假設(shè)中,A 只有在處理大多數(shù)不同情形時能得到全局最優(yōu)解,才能被稱為「可認證算法」,滿足自動駕駛的安全需求。
2. " 非凸 " 轉(zhuǎn) " 凸 "
2018 年 12 月,楊珩加入麻省理工學(xué)院信息與決策系統(tǒng)實驗室(Laboratory for Information & Decision Systems, LIDS),師從 MIT 萊納多職業(yè)發(fā)展副教授 Luca Carlone,開始從事計算機視覺與機器人的結(jié)合研究。
一開始,他們只是從一個小的點云配準(zhǔn) / 重建(point cloud registration)問題出發(fā)。所謂 " 點云配準(zhǔn) ",指的是求兩個點云之間的旋轉(zhuǎn)平移矩陣,將源點云變換到與目標(biāo)點云相同的坐標(biāo)系下。比如,一輛車無人車分別處在 a 點與 b 點,用無人車點雷達分別對著一棟樓掃一下,再把兩張掃描的圖融合在一起。
他們針對這個問題設(shè)置了一個可認證算法,并在 2019 年 1 月投了一篇文章到機器人頂會 RSS(Robotics: Science and System),文章被接收。在這篇工作中,他們使用 TLS 來重新設(shè)計點云優(yōu)化估測問題,使估計對大部分虛假的點到點對應(yīng)關(guān)系不敏感,可以容忍高達 99% 的異常值(outliers)。
圖注:楊珩被 RSS 2019 接收的工作,論文地址為 https://arxiv.org/pdf/1903.08588.pdf
但是,他們在 RSS 2019 中提出的可認證算法精確度并不夠突出,有時無法滿足上述所說的第三個條件(對大部分輸入數(shù)據(jù)都能獲得最優(yōu)解)。許多時候,該算法得到的差距至多是 1e-2、1e-3,而不是 1e-6 或 1e-10 等接近 0 的差距。
從 RSS 2019 開始,他們就一直在研究可認證算法。
2019 年 2 月左右,楊珩用兩周時間獨自琢磨,看了許多數(shù)學(xué)資料,嘗試換一種對原問題(TLS)的求解方法。他從一個數(shù)學(xué)思維出發(fā),提出了半正定規(guī)劃(Semidefinite Programming)松弛,將非凸優(yōu)化問題 TLS 轉(zhuǎn)化為凸優(yōu)化問題。這個方法十分成功,他們投到了 ICCV 2019,被成功接收。

圖注:楊珩被 ICCV 2019 接收的工作,論文地址為 https://arxiv.org/pdf/1905.12536.pdf
對楊珩來說,ICCV 2019 的這篇工作有里程碑式的紀念意義:因為那篇文章是第一個能將有異常值(outliers)的機器人感知問題在多項式時間內(nèi)(polynomial time)解到全局最優(yōu)(global optimality)的工作。我們設(shè)計的半正定規(guī)劃松弛(SDP relaxation)是 extremely tight,那個算法幾乎對所有問題都能得到全局最優(yōu),而且它解的原問題是一個帶有二元變量(+1 和 -1,mixed integer)的非凸問題。這種問題是一個 NP-hard 問題。
Wahba 問題,又稱為 " 旋轉(zhuǎn)搜索 ",旨在找到最佳旋轉(zhuǎn)以在給定的對應(yīng)關(guān)系下對齊兩組向量觀察,是許多計算機視覺和機器人應(yīng)用中的基本研究(比如可以用作衛(wèi)星的定位)。在 ICCV 2019 中,楊珩針對大量向量觀測值為異常值(outliers)的情況,提出了第一個多項式時間可證明的最優(yōu)方法來解決 Wahba 問題。
在這篇工作中,除了使用 TLS 成本來制定 Wahba 問題,他們還開發(fā)了凸半定規(guī)劃(SDP)松弛來解決非凸問題。他們提出可認證算法 QUASAR (基于 QUAternion 的半定松弛法,用于魯棒對齊),即使在面臨大量噪聲與異常值的情況下(比如多余 95% 的異常值),他們的松弛也很 " 緊 ",算出可證明的全局最優(yōu)解(即松弛是精確的),優(yōu)于魯棒的局部優(yōu)化算法 RANSAC。
" 非凸 " 轉(zhuǎn) " 凸 ",是楊珩提出的算法能夠在大部分輸入數(shù)據(jù)中求得全局最優(yōu)解的關(guān)鍵點。憑借這一主導(dǎo)思想以及后續(xù)的一系列工作,楊珩獲得 ICRA 2020 的機器視覺最佳論文獎,還入圍了 RSS 2021 最佳論文獎最終名單。
如前所述,TLS 是一個非凸優(yōu)化問題,基本框架如下:
非凸問題幾乎是無法快速求得全局最優(yōu)解的,但是,我們可以通過凸松弛方法,將非凸問題轉(zhuǎn)為凸問題。這個過程就相當(dāng)于以退為進:當(dāng)你面對一道難題(如非凸問題)、不知所措時,你可以先把它轉(zhuǎn)化成一個較為簡單的問題(如凸問題),然后去求解這個簡單的問題。解完簡單的問題后,你會知道簡單的問題 B 與原問題 A 是否等價。
更有意思的是,在解出簡單問題 B 之前,你并不知道簡單問題 B 是否與難問題 A 是否等價。但當(dāng)你解完 B 后,你會檢驗該解是否滿足原問題的某些條件、從而推測問題 B 與問題 A 是否等價。如果滿足,那么凸問題被解,實際上也就意味著原來的非凸問題已經(jīng)解決。
「有點 " 事后諸葛亮 " 的感覺。」楊珩形容。從理論上講,一般性的凸問題也是 NP-hard 問題,目前在多項式時間內(nèi)是不可求解的,但極個別凸問題,比如 SDP 的優(yōu)點是:可以在多項式時間內(nèi)求出全局最優(yōu)解。在這個凸問題中,所有局部最優(yōu)都是全局最優(yōu)。
在 " 非凸 " 轉(zhuǎn) " 凸 " 的過程中,楊珩的靈感也源自一個非常著名的數(shù)學(xué) " 松弛 " 理論:2001 年,法國數(shù)學(xué)家 Jean B. Lasserre 在數(shù)學(xué)頂刊《SIAM Journal on Optimization》上發(fā)表了一篇著名的文章,叫 "Global optimization with polynomials and the problem of moments"(引用量已超過 2600),里面提到:
非凸問題永遠不可能等價于凸問題,但如果滿足一定條件,我們就可以用一個足夠大的凸問題來逼近 / 解決一個非凸問題。不過,我們并不明確該非凸問題有多大,它可能是無限大。
這是一個十分優(yōu)美的理論。假設(shè)非凸問題是迷霧中的一座小島,那么凸問題就是一片不斷在尋找島嶼邊界的汪洋,摸索,定義,直至幾乎全部包圍,不斷接近真實的全貌。
但也不難推測,在這個 " 松弛 " 的過程中,研究會面臨兩個難點:
1)如何用一個足夠小的凸問題來解決非凸問題?比方說,原來的非凸問題可能只有 100 個參數(shù)要求解,但你要解的凸問題可能有 100 萬個參數(shù)。也就是說,你需要解一個非常大的凸問題,才能解原來的非凸問題。
2)楊珩觀察到,雖然只要解決一個包含 100 萬參數(shù)的凸問題、就能解原來只有 100 個參數(shù)的凸問題,但目前在數(shù)學(xué)上,沒有一個求解器可以解決這么大的凸問題。在楊珩的研究中,他所用于求解非凸問題的凸問題是 " 半正定規(guī)劃 " 問題(Semidefinite Programming, SDP),屬于凸問題里最難的一類。
從理論上講,要解決原來的非凸問題 TLS,轉(zhuǎn)換的凸問題可能要無限大,不止 100 萬個參數(shù),也可能是 1000 萬、1 億、10 億甚至上百億。針對第一個難點,楊珩及團隊用真實計算顯示:轉(zhuǎn)化的凸問題(即 SDP 問題)不需要無限大,只需要一個最小的凸問題(參數(shù)量為 100 萬 ) ,即可解決原來的非凸問題。
而且,在將非凸問題(下圖左)轉(zhuǎn)為凸問題(下圖右)的過程中,算法不僅在凸問題上求解,還會將凸問題的解投射到原來的非凸問題中,來回求解。在這個過程中,非凸問題的解會加速凸問題的求解,非凸問題的局部最優(yōu)也可以映射到凸問題的頂點(vertexes),加速求解。目前,他們的工作是第一次在 SDP 求解中用到了這種「不舍原問題」的求解思想,極具創(chuàng)新。

而對于第二個難點,楊珩他們所面臨的難點是:目前市面上現(xiàn)有的求解器最多只能求解規(guī)模為小到中等的 SDP 問題。所以,他們只能自己研發(fā)求解器。
3. 研發(fā)求解器 STRIDE
找到全局最優(yōu)解,與證明全局最優(yōu)解,是兩碼事。比如,在 ICRA 2020 的機器視覺最佳論文獎中,楊珩所提出的算法便能快速找到全局最優(yōu)解,但是無法證明該解是全局最優(yōu),即找不到一個明確的 " 證書 "(certificate)來佐證。
楊珩解釋,從本質(zhì)上看,Robotics(關(guān)于機器的學(xué)科)的核心是優(yōu)化,車輛的 3D 姿態(tài)估計便是在解一個優(yōu)化問題。不僅是感知,自動駕駛中的車輛控制、規(guī)劃等,都是在解決優(yōu)化問題。
針對不同的優(yōu)化問題,研究人員會使用不同的優(yōu)化框架,并根據(jù)某個特定的框架尋找是否有合適的求解器。研究分為兩步進行:建模(modeling)與求解(solving)。
所謂「建模」,就是將一個真實世界的問題(如上述所說的自動駕駛汽車感知周圍事物)轉(zhuǎn)化為一個數(shù)學(xué)問題。建模完成后,解決這個數(shù)學(xué)優(yōu)化問題的過程就叫做「求解」。一般情況下,目前在機器人(Robotics)領(lǐng)域,大多數(shù)工作都是只做建模,僅依靠現(xiàn)存的求解器來解決數(shù)學(xué)上的優(yōu)化問題。楊珩的博士導(dǎo)師 Luca Carlone 此前便主要做建模。
但在研究可認證算法的過程中,他們發(fā)現(xiàn),如果只做建模是無法解決 100 萬參數(shù)量的問題。市面上也沒有成熟的 SDP 求解器可以幫助他們解決這個問題,所以他們只能自己去開發(fā)求解器。
從 2019 年開始,他們就在尋找適合的求解器。一開始,他們的問題也沒有包含那么多的變量,現(xiàn)有求解器已能滿足這個凸問題的計算要求。直到去年 9 月,他們的研究要面臨越來越多的參數(shù)量,才發(fā)現(xiàn)「還是得自己開發(fā)求解器,因為現(xiàn)有的求解器解決不了我們的問題。」
從去年 9 月到今年 4 月,他們一直在嘗試不同的求解器,發(fā)現(xiàn)結(jié)果均不盡如人意。于是,他們就去找了新加坡國立大學(xué)數(shù)學(xué)系的系主任 Kim-Chuan Toh 和他的學(xué)生 Ling Liang,與他們一起合作,針對待解凸問題的特質(zhì),用大約 4 個月的時間開發(fā)出了一個主要面向 SDP 問題的約束求解器—— STRIDE。(STRIDE 的源碼目前已在 Github 上公開:https://github.com/MIT-SPARK/STRIDE)
開發(fā)求解器的難點,主要是利用好待解決問題的優(yōu)勢。半正定規(guī)劃(SDP)是一個很大的數(shù)學(xué)問題,而楊珩要解決的 SDP 問題除了通用特征,還有一些特殊的性質(zhì)。比如,它的最優(yōu)解是低階(low rank)。
而有了 STRIDE 的助力后,楊珩所提出的可認證感知算法在求解速度與準(zhǔn)確度上均有了明顯的提升。
如下圖所示,原來的非凸問題 TLS 只有 54 個變量時,它所對應(yīng)的凸問題 SDP 至少有 8154 個變量;TLS 只有 1004 個變量時,SDP 問題的變量超過了 300 萬。MOSEK 與 SDPT3 被視為目前最出色的 SDP 求解器,但隨著問題的變量越來越多,MOSEK 與 SDPT3 不僅無法求解,甚至連存儲該問題的內(nèi)存都沒有。

在上圖中,1e-10、1e-12 等數(shù)值為精確度。數(shù)值越低,求解的精確度越高。從第 1 行到第 5 行,優(yōu)化的問題越來越大,測度(measurement)越來越多。回到一開始的例子,就是自動駕駛車輛周圍的汽車越來越多,汽車的關(guān)鍵點與連線也會越來越多。
實驗證明,當(dāng)問題的維度(dimension)較低時,SDPT3 和 MOSEK 可以求解,但速度不到 STRIDE 的二分之一。比如,在維度為 104 時,MOSEK 的求解時間是 870 秒,而 STRIDE 只需 45 秒;維度為 204 時,MOSEK 無法求解,而其他算法雖然可以解,但卻解不到全局最優(yōu),精確度不夠。當(dāng)維度達到 1004 時,即使給再多的運行時間,其他求解器也無法達到與 STRIDE 相匹配的精確度。
楊珩介紹,他們所提出的算法是目前唯一能夠解決大規(guī)模一階(rank-one)SDP 問題的方法。他們在百度的自動駕駛數(shù)據(jù)集 Apollo Scape (圖像采集自北京、上海與深圳)上做過實驗,STRIDE 的性能明顯優(yōu)于 MOSEK 等求解器。

此前,他們的工作曾發(fā)表在 NeurIPS 2020 上,但當(dāng)時,算法只解決了 4 個常見的感知問題。加上 STRIDE 后,他們嘗試將算法拓展至更廣泛的設(shè)置下進行,解決了 6 個感知問題,包括單點旋轉(zhuǎn)均勻(single rotation averaging)、多點旋轉(zhuǎn)均勻(multiple rotation averaging)、點云配準(zhǔn)、網(wǎng)格配準(zhǔn)、絕對姿態(tài)估計與分類感知。

求解器的核心思想是優(yōu)化與決策,而自動駕駛的運行就是 "robot"(汽車)一直在做決策。比如,自動駕駛車輛要從 a 點走到 b 點,而 a 點與 b 點之間有一個障礙物,那么,規(guī)劃一條從 a 點到 b 點的最短路線,便是一個近似優(yōu)化問題。
楊珩還介紹,STRIDE 求解器不僅可以解決機器視覺問題,還有望解決一些數(shù)學(xué)問題。他們最近做了一些新的工作,便計劃投到數(shù)學(xué)類的期刊與會議上。
4. 數(shù)學(xué)不可或缺
目前,楊珩的工作還處于學(xué)者討論的階段,距離落地還有一段很長的距離。
盡管他們的算法在求解速度上已經(jīng)很快,但實際的求解時間也要 1 個小時。如果可認證算法要在現(xiàn)實中落地,那么求解時間至少要從 1 個小時縮減到 1 秒。雷鋒網(wǎng)
「很多人認為自動駕駛很簡單,那或許是因為他們還沒有體會到數(shù)學(xué)和科學(xué)計算有多難。」楊珩感嘆,「從 L1 到 L5,自動駕駛要解決的都是數(shù)學(xué)問題。越來越多人發(fā)現(xiàn),自動駕駛不是只依靠神經(jīng)網(wǎng)絡(luò)就能成功。」雷鋒網(wǎng)
盡管如此,楊珩的可認證感知算法仍有存在的意義:「我可以認證,只是我現(xiàn)在認證的時間比較長而已。」在未來,計算硬件的提升可能會帶來問題的突破。
對楊珩等癡迷理論研究的科研者來說,在研究可認證算法的過程中,「非凸」轉(zhuǎn)「凸」的成功,才是一件比求解時間從 1 小時縮減到 1 秒更令人激動的突破。
在研究的過程中,楊珩受到許多數(shù)學(xué)知識的幫助與啟發(fā),也取得了不少突破性的成果。因此,他覺得數(shù)學(xué)在視覺算法研究(和其他科學(xué)研究)中是一門十分重要的學(xué)科:
硬核數(shù)學(xué)問題會非常考驗人的耐心。我覺得有時候也不是難不難的問題,而是你能不能花一天的時間看一篇數(shù)學(xué)文章,搞懂這篇文章的所有細節(jié)。有可能你看了 5 遍之后,你就會醍醐灌頂。在那一瞬間,這個方法成為了你自己的方法。一旦你掌握了這個方法之后,你就會發(fā)現(xiàn)這個方法特別地 powerful(強大),可以將它應(yīng)用到很多別的方案中。雷鋒網(wǎng)
如果有一天,你能想明白數(shù)學(xué)家是怎么理解問題的,可能你的境界就高了一層。
談到未來的研究方向,楊珩的愿望之一是用可認證算法來指導(dǎo)神經(jīng)網(wǎng)絡(luò)的訓(xùn)練過程,提高神經(jīng)網(wǎng)絡(luò)的安全性。
少年新馬,未來可期。