我們知道,計算機使用的是二進制計數法。也就是說,在計算機中的所有信息都是使用二進制來存儲和處理的。
下表列出了我們熟悉的十進制數及與其相對應的二進制數:

位運算規則
在位運算中,“按位與”運算(AND運算)分別按位比較兩個相應的數字(0或1),當且僅當這兩個數字都為1時,結果才為1,如下式所示:

可以看出,實現“按位與”運算,就是將對應位置的數相乘。因此,從右自左的第1個位置是1*1=1,第2個位置是0*1=1,等等,最后得到結果。
除了“按位與”運算外,還有按位或(OR)、異或(XOR)、蘊含(IMP)、相等(EQ)和非(NOT)運算,它們都有不同的運算規則。例如,對于OR運算來說,當兩個數字至少有一個為1時,結果為1,如下式所示:
![]()
同理,可以看出,實現“按位與”運算,就是將對應位置的數相加,結果為正數就是1,結果為零就是0。因此,從右自左第1個位置是1+1=2,即為1,第2個位置是0+1=1,就是1,等等,最后得到結果。
其他的位運算規則可以參閱相關資料,下面主要以“按位與”和“按位或”為例,解如何在Excel中實現位運算。
將十進制數轉換成二進制數
有時候,在Excel工作表中實現位運算是非常有用的,然而,Excel并沒有直接用于位運算的函數,這就需要我們組合一些函數來實現位運算功能。
下面,以處理0至255之間的十進制數為例。
在將0至255之間的十進制數轉換成二進制數時,需要的二進制數的位數是8位。例如,十進制數0的二進制數表示為:
00000000
十進制數255的二進制數表示為:
11111111
可以使用下面的公式來獲得十制數相對應的二進制數的每一位(0或1):
=MOD(INT(十進制數/(2^(二進制數所處的位置值-1))),2)
也就是說,要求二進制數中的其中一位,先求2對該位所在的位置值減1的冪,然后由其十進制數除以所求冪的結果,對求得的結果取整,并作為MOD函數的參數求其對2的余數,即為該位所在的二進制數(0或1)。
下圖1演示了在Excel工作表中使用公式將十進制數222轉換成二進制數11011110的過程。
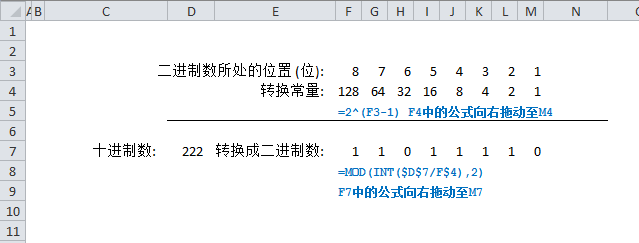
圖4
結語
位運算可以用來實現很多令人驚嘆的電子表格設計,解決很多具有挑戰性的問題,待我進一步學習后與大家分享。






