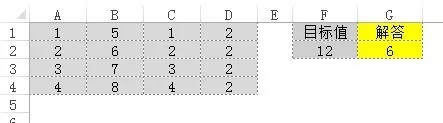
如下圖1所示,在一個4行4列的單元格區域A1:D4中,每個單元格內都是一個一位整數,并且目標值單元格(此處為F2)也為整數,要求在單元格G2中編寫一個公式返回單元格A1:D4中四個不同值的組合的數量,條件如下:
1. 這四個值的總和等于F2中的值
2. 這四個值中彼此位于不同的行和列
這正是我們要生成的27個排列。
對于以10為底的給定值,為了確定該值的以3為底的表示形式中存在的3^2、3^1和3^0的數量,首先確定3^2、3^1和3^0的以基數為10的值,然后對所得值取模(模為3)。例如,以10為底的值7,以3為底的值的表示形式為021,由于3^2=9在7中出現0次且MOD(0,3)=0,3^1=3在7中出現2次且MOD(2,3)=2,3^0=1在7中出現1次且MOD(1,3)=1。這意味著:
MOD(INT((ROW(1:27)-1)/3^{2,1,0}),3)
轉換為:
{0,0,0;0,0,1;0,0,2;0,1,0;0,1,1;0,1,2;0,2,0;0,2,1;0,2,2;1,0,0;1,0,1;1,0,2;1,1,0;1,1,1;1,1,2;1,2,0;1,2,1;1,2,2;2,0,0;2,0,1;2,0,2;2,1,0;2,1,1;2,1,2;2,2,0;2,2,1;2,2,2}
然后,使用MMULT和合適的第二個數組將該數組合并為10為底的值:
MMULT(MOD(INT((ROW(1:27)-1)/3^{2,1,0}),3),10^{2;1;0})
轉換為:
MMULT({0,0,0;0,0,1;0,0,2;0,1,0;0,1,1;0,1,2;0,2,0;0,2,1;0,2,2;1,0,0;1,0,1;1,0,2;1,1,0;1,1,1;1,1,2;1,2,0;1,2,1;1,2,2;2,0,0;2,0,1;2,0,2;2,1,0;2,1,1;2,1,2;2,2,0;2,2,1;2,2,2},{100;10;1})
得到:
{0;1;2;10;11;12;20;21;22;100;101;102;110;111;112;120;121;122;200;201;202;210;211;212;220;221;222}
最后,使用TEXT函數格式化以生成所需要的排列:
TEXT(MMULT(MOD(INT((ROW(1:27)-1)/3^{2,1,0}),3),10^{2;1;0}),”000″)
得到結果:
{“000″;”001″;”002″;”010″;”011″;”012″;”020″;”021″;”022″;”100″;”101″;”102″;”110″;”111″;”112″;”120″;”121″;”122″;”200″;”201″;”202″;”210″;”211″;”212″;”220″;”221″;”222”}
小結
1.找到規律,然后尋求解決之道。
2.不僅要理解Excel函數原理,而且要打好數學基礎,這是靈活應用公式的一切。






