排序算法有很多,像冒泡排序,選擇排序,插入排序,希爾排序,快速排序等等。今天這篇文章呢,我們來聊一聊簡單的冒泡排序(Bubble Sort)。

想必大家都知道魚吐泡泡的現(xiàn)象,氣泡從魚的嘴巴里面呼出來,一個一個的往水面上冒出去。這是因為呀,氣泡里面的擁有大量的二氧化碳,而二氧化碳比水要輕,所以氣泡可以一個一個的往水面上浮動。
而我們今天要講的冒泡排序與“魚吐泡泡”現(xiàn)象有些相像,所以呢,我們可以把冒泡排序與該現(xiàn)象進行類比學習。
相比于“魚吐泡泡”現(xiàn)象,冒泡排序的原理就是通過一次次的比較,將較大(較小)的元素向著數(shù)組的一側移動。經過數(shù)次移動以后,數(shù)組中的元素就會按照從小到大(從大到小)排列起來。
了解了這些后,冒泡排序具體該怎么實現(xiàn)移動的動作呢,讓我來給大家慢慢演示一遍:
有一個數(shù)組,里面存儲著8個無序的數(shù)字,我們要做的就是將它們進行從小到大的順序進行排列。

根據(jù)冒泡排序的思想,我們要把相鄰的兩個元素進行比較,因為要進行從小到大排序,如果前一個數(shù)比后一個數(shù)要大,那么我們就要交換兩元素的位置;如果前一個數(shù)比后一個數(shù)要小或者相等,那么就無須交換元素,接著向下比較就好了。
例如:
首先是第一個數(shù)5與第二個數(shù)8進行比較, 5 < 8 , 則元素位置無須變化。
接下來讓8和6進行比較,8 > 6 , 要交換8和6的位置。
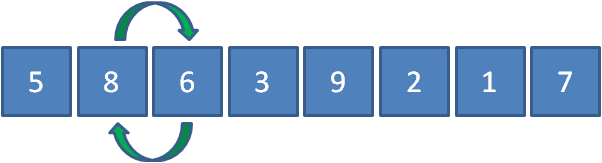

然后再讓8和3比較,8 > 3 , 所以交換8和3的位置。


再讓8和9進行比較,8 < 9 , 元素位置不用改變。
接著再讓9和2進行比較, 9 > 2 , 交換9和2的位置

接下來讓9和1進行比較,9 > 1, 交換9和1的位置。

最后再讓9和7進行比較,9 > 7 , 交換9和7的位置。

經過7次比較,我們選出了這8個元素中最大的元素—— 9,并且將元素9,像冒泡泡一樣往上浮動,放在了數(shù)組的最后面。
這樣,我們的第一輪冒泡排序已經結束,并且將元素9放在了最后,相當于形成了一個有序區(qū),只不過此時的有序區(qū)只有一個元素9。

那么,現(xiàn)在我們再進行第二輪冒泡排序:
首先是5和6比較,5 < 6 , 元素位置不變。
再讓6和3比較, 6 > 3 , 交換6和3的位置。


接著讓6和8比較,6 < 8, 元素位置不變。
然后再讓8和2進行比較,8 > 2, 交換8和2的位置。

接著再讓8和7進行比較, 8 < 7, 交換8和7的位置。

因為9已經是有序區(qū)里面的元素了,無須參與第二輪比較,所以第二輪冒泡排序經過6次比較,選出了最大元素—— 8,隨之將8算進有序區(qū)內。

按照相同的邏輯,我們可以得到:
第三輪冒泡排序結果:

第四輪冒泡排序結果:

第五輪冒泡排序結果:

第六輪冒泡排序結果:

第七輪冒泡排序結果:

第八輪冒泡排序結果:

經過8輪冒泡排序后,元素已經按照從小到大順序排列在數(shù)組內,也可以說有序地排列在有序區(qū)內。
由于該排序算法的每一輪要遍歷所有元素,輪轉的次數(shù)和元素數(shù)量幾乎相同,所以時間復雜度是O(N^2)
冒泡排序是一種穩(wěn)定排序,也就是說當存在兩個相同元素時,比如1, 2, 1, 3, 5.存在相同的兩個元素——1,穩(wěn)定排序說的就是在經歷過多次排序,形成有序數(shù)列以后,相同元素的相對位置依然未改變。
排序前:1(第一個1), 2, 1(第二個1), 3, 5;
排序后:1(第一個1), 1(第二個1), 2, 3, 5。
排序前的第一個1就是排序后的第一個1;排序前的第二個1也就是排序后的第二個1。沒有出現(xiàn)前一個1跑到后面去,后一個1跑到前面去的現(xiàn)象,所以說冒泡排序是一種穩(wěn)定的排序。
下面是冒泡排序的代碼實現(xiàn):
//冒泡排序(從小到大)
public class Sort1 {
public static void main (String[] args) {
int[] arr = new int[] {5, 8, 6, 3, 9, 2, 1, 7};
sort(arr);
System.out.println("冒泡排序完畢后:" + Arrays.toString(arr));
}
public static void sort (int[] arr) {
for (int i = 0; i < arr.length; i++) { //比較輪次
for (int j = 0; j < arr.length - i - 1; j++) { //每一輪的比較次數(shù)
// 交換元素,大的值往后移
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
}
程序執(zhí)行結果:
冒泡排序完畢后:[1, 2, 3, 5, 6, 7, 8, 9]
改進:
請大家看一看,后三輪的排序狀態(tài)。
第六輪冒泡排序結果:

第七輪冒泡排序結果(元素已經有序):

第八輪冒泡排序結果(元素已經有序):

沒錯,后三輪排序的弊端在于,元素已經有序了,然而冒泡排序還在進行比較,這樣的比較無疑是浪費時間的。
我再舉一個較為極端的例子:我給出一個長度為8的數(shù)組:

這個數(shù)組,在使用冒泡排序時,第一輪過后,元素已經變得有序:

那么后面的7輪排序其實是在做“無用功”。因此我們要防止這種無意義的比較發(fā)生,我們需要對上述冒泡排序代碼進行一些改動。
其實改動也比較簡單,我們只需要加上一個變量isSorted,來判斷元素是否已經有序即可。
改進代碼:
//改進冒泡排序(從小到大)
public class Sort1 {
public static void main (String[] args) {
int[] arr = new int[] {5, 8, 6, 3, 9, 2, 1, 7};
sort(arr);
System.out.println("冒泡排序完畢后:" + Arrays.toString(arr));
}
public static void sort (int[] arr) {
for (int i = 0; i < arr.length; i++) { //比較輪次
boolean isSorted = true; //元素是否有序的判斷變量
for (int j = 0; j < arr.length - i - 1; j++) { //每一輪的比較次數(shù)
// 交換元素,大的值往后移
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
isSorted = false; //發(fā)生了元素交換,isSorted賦值為false
}
}
if (isSorted) //一輪冒泡排序后,如果發(fā)生了交換isSorted為false,否則為true
break; // 如果未發(fā)生交換,說明元素有序,直接退出循環(huán),反之進行下一輪
}
}
}
以上便是我對冒泡排序的理解,感謝小伙伴們的閱讀!






