01
故事起源
幼兒園放學(xué),小朋友們集合,需要先從低到高排隊(duì),應(yīng)該怎么排呢?

02
開始行動(dòng)
小K身高180,是班里最高的,自然得往后排啦。小K先和身后的小B比較,然后和小B交換。

小K接著和身后的小D比較,然后和小D交換。

經(jīng)過和4個(gè)小朋友交換位置,小K終于找到自己的位置啦。

上面的過程其實(shí)就是冒泡排序的核心思想了。
03
冒泡排序
為描述方便,用下面的數(shù)組模擬小朋友的交換過程。
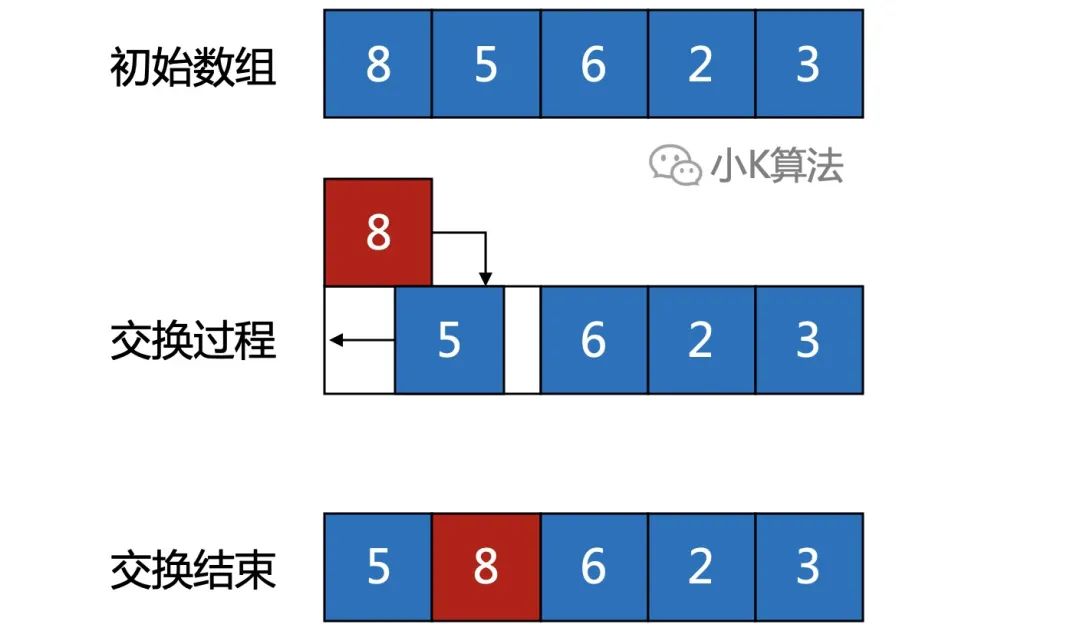
核心思想(升序):
從首位置開始,依次比較前后兩個(gè)數(shù),如果前面的數(shù)比后面的數(shù)大,就交換兩個(gè)數(shù)。這樣第1輪結(jié)束后,最大的數(shù)就會移動(dòng)到最后的位置。對剩余元素重復(fù)執(zhí)行N-1次,整個(gè)數(shù)組有序。因?yàn)橄窨諝馍细〉剿妫畲蟮脑貢〉阶詈螅悦芭菀虼说妹?/p>
3.1
第1輪
執(zhí)行完成后,最大的元素歸位。
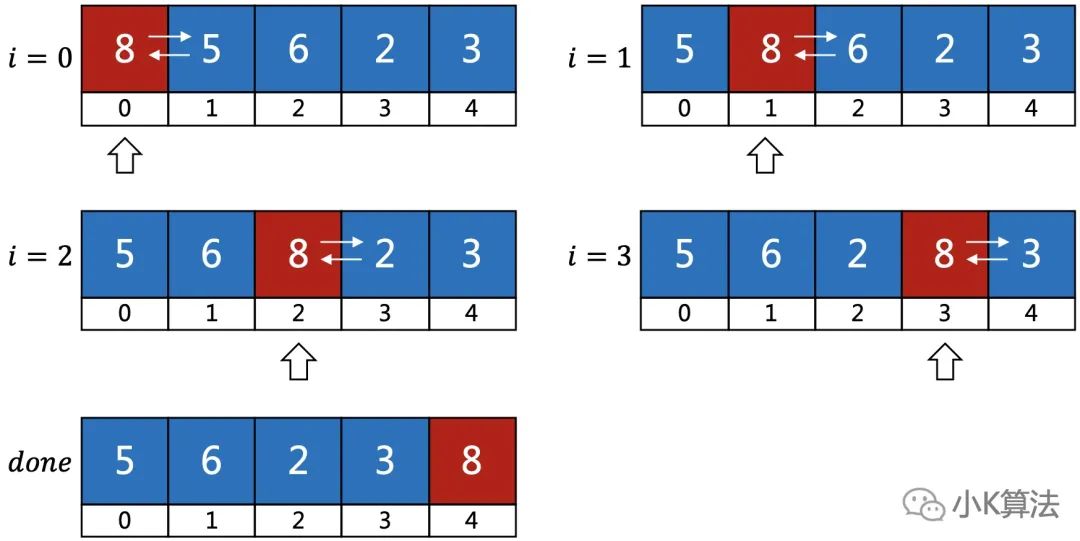
3.2
第2輪
第2輪接著對前面剩余的N-1個(gè)元素重復(fù)上面步驟,第2大的元素歸位。
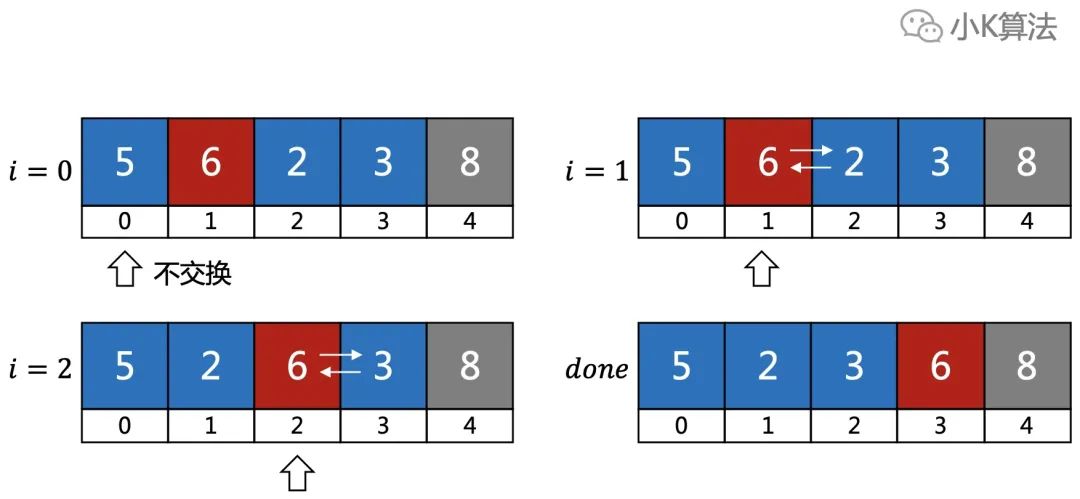
3.3
第3輪
第3輪對前面剩余的N-2個(gè)元素重復(fù)上面步驟,第3大的元素歸位。

總共執(zhí)行N-1次操作,所有元素歸位。
3.4
代碼實(shí)現(xiàn)
for (int i = 0; i < n - 1; ++i) {
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j + 1]) {
swap(a[j], a[j + 1]);
}
}
}
04
問題及優(yōu)化
4.1
迭代輪次優(yōu)化
如果原數(shù)組為如下情況,那么在執(zhí)行完第1輪后,整個(gè)數(shù)組已經(jīng)有序,后面的輪次沒必要執(zhí)行,可以針對這種情況做一次優(yōu)化改進(jìn)。
改進(jìn)點(diǎn)1:
如果某一輪沒有發(fā)生過交換,說明數(shù)組已經(jīng)有序,那么以后也不會發(fā)生交換,此時(shí)可以終止迭代。

代碼實(shí)現(xiàn)
for (int i = 0; i < n - 1; ++i) {
// flag標(biāo)記是否有交換
bool flag = true;
for (int j = 0; j < n - i - 1; ++j) {
if (a[j] > a[j + 1]) {
swap(a[j], a[j + 1]);
flag = false;
}
}
if (flag) {
break;
}
}
4.2
掃描范圍優(yōu)化
如果為以下情況,我們會發(fā)現(xiàn)最后的6和8所處的位置和最終排序完成的位置一樣,說明過程中他們的位置不會發(fā)生變化。
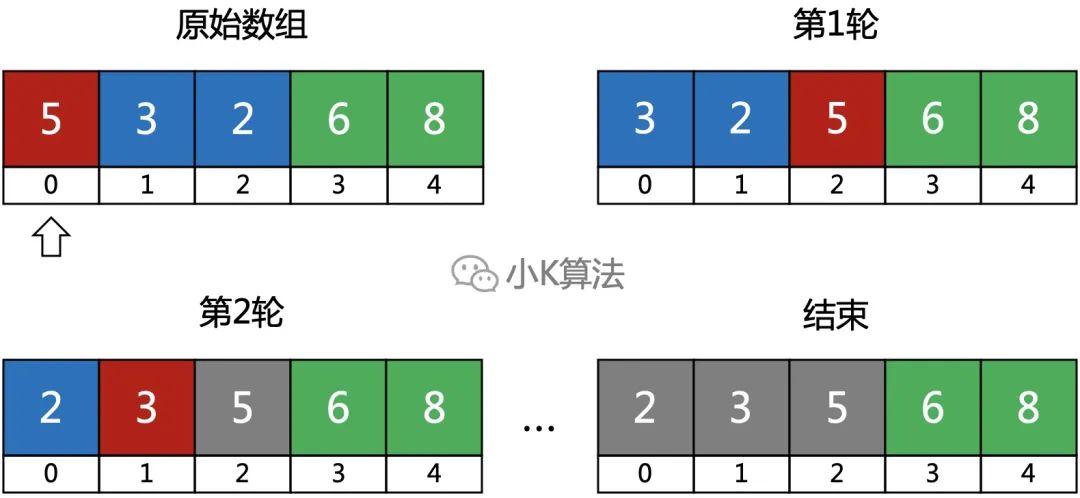
上一輪最后交換的位置,在下一輪時(shí),此位置后面的數(shù)也不會再發(fā)生交換。

改進(jìn)點(diǎn)2:
記錄每一次最后發(fā)生交換的位置,下一輪只需要掃描到此位置的前一個(gè)即可。
代碼實(shí)現(xiàn)
// 記錄最后交換的位置
int position = 0;
int len = n - 1;
for (int i = 0; i < n - 1; ++i) {
// flag標(biāo)記是否有交換
bool flag = true;
for (int j = 0; j < len; ++j) {
if (a[j] > a[j + 1]) {
swap(a[j], a[j + 1]);
flag = false;
position = j;
}
}
len = position;
if (flag) {
break;
}
}
05
總結(jié)
冒泡排序是比較簡單的一種排序算法,核心思想就是比較相鄰的兩個(gè)數(shù),但效率比較低所以可做一些優(yōu)化。時(shí)間復(fù)雜度為O(N^2),數(shù)據(jù)規(guī)模較小時(shí)可采用,但數(shù)據(jù)過大時(shí)就不建議采用冒泡了。
來源:小K算法
作者 :小K
原標(biāo)題:圖解算法:冒泡排序
編輯:hxg、yrLewis






