來源：EETOP論壇 及 不忘初心的模擬小牛牛公眾號
作者：131v1vv
一直想對積分變換的內(nèi)容做一個比較系統(tǒng)的總結(jié)和歸納，可能是源于大學對信號與系統(tǒng)的渣渣學習吧。
相信不管是做模擬，混合信號還是射頻，《信號與系統(tǒng)》都是基礎內(nèi)容，且重要性極高，難度也很大，相信有不少從小抱著要從事IC設計這種高（搬）大（磚）上（工）專業(yè)或職業(yè)的人都栽在了學習信號與系統(tǒng)的道路上，僥幸拿到60分的估計考完后再也沒有動力撿起來了，像我這種學渣，僥幸入了坑，才發(fā)現(xiàn)出來混遲早要還的。既然躲不過，那就硬著頭皮從頭來過咯。
借這個機會，準備把積分變換的相關(guān)內(nèi)容系統(tǒng)的總結(jié)一下，順便也在好好學習思考。如果單單把oppenheim的書本內(nèi)容抄過來，肯定會很枯燥，被本科這種填鴨式教學給幼小的心靈留下的創(chuàng)傷之后，肯定不想在被傷害一次吧。所以我試著盡可能用比較少的公式，把相關(guān)內(nèi)容呈現(xiàn)出來。如果在被我寫的內(nèi)容傷害，那可是罪過啊。也表示一下歉意。
我們先總括的把相關(guān)知識及相互關(guān)系和基礎知識羅列出來。
這里不得不先聊聊歐拉，歐拉（Leonhard Euler，1707-1783），生于瑞士。具有開掛的一生，在18世紀的科學史上留下太多傳說。興趣廣泛，成就也很多。其中在復變函數(shù)的歐拉公式(Euler's formula)，更是基礎內(nèi)容。
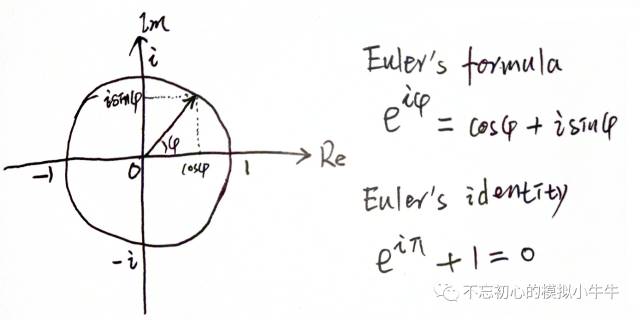
圖1
圖1中的歐拉公式，建立了復指數(shù)(complex exponential)和三角函數(shù)的關(guān)系。在數(shù)學、物理和工程中無處不在，我們要講的積分變換中會經(jīng)常見到。該公式可以使用泰勒級數(shù)展開進行證明。其中當φ=π時，歐拉公式進化為歐拉恒等式(Euler's identity)。這是數(shù)學中最令人著迷的公式。聯(lián)系了自然常數(shù)e，圓周率π，虛數(shù)單位i、實數(shù)的0和1。高斯曾有過類似感嘆：“一個人第一次看到這個公式而不感到它的魅力，他不可能成為數(shù)學家。”盡管我這榆木的腦袋，是沒有可能成為數(shù)學家啦，但不影響欣賞美的態(tài)度。
虛數(shù)單位i將實數(shù)擴展到復平面，歐拉公式把二維平面的點，從直角坐標到極坐標表示。這里借鑒wikipedia繪出歐拉公式的三維圖，紅色螺旋線。其在Re平面投影為Cos余弦函數(shù)，在Im平面投影為Sin正弦函數(shù)。相信大家有學過電磁場會有印象，電磁波的傳播過程中，電場和磁場正交。其中紅色的部分的螺旋線也有點像DNA的結(jié)構(gòu)，很神奇。
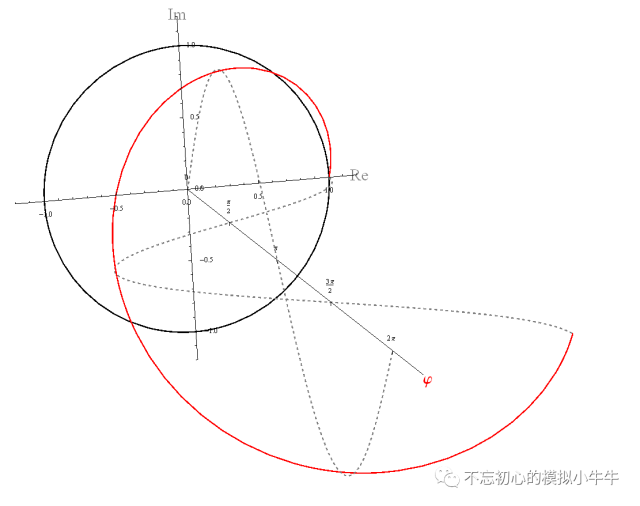
圖2
對歐拉公式變型，可以將三角函數(shù)表示為復指數(shù)的形式，如圖3所示。
圖3
在18世紀中葉，歐拉在研究振動弦問題時，嘗試通過線性組合不同諧波的三角函數(shù)來表示質(zhì)點振動問題。也經(jīng)過激烈的討論，有了逐漸認識和完善的過程。其中就包括伯努利，拉格朗日、傅里葉等人。特別是傅里葉在不利的背景下。深入研究了該問題，特別是非周期信號可以表示為不全成諧波關(guān)系的正弦信號的加權(quán)積分。以此激勵人們更深入的研究該問題。為紀念傅里葉的突出貢獻，以他的名字命名了傅里葉級數(shù)和傅里葉變換。
周期為T的信號，其傅里葉級數(shù)表示如圖4所示。傅里葉級數(shù)系數(shù)為ak，其中a0成為直流分量，a±1為一次諧波分量，a±k為k次諧波分量。
圖4
對于圖4的周期信號傅里葉級數(shù)展開，相信大家對課本上的方波信號的展開都有印象，這里舉個三角波信號，如圖5所示。其中實信號的周期為2，在區(qū)間[-1,1]的定義為三角波。傅里葉級數(shù)系數(shù)的幅度如圖6所示。
圖5
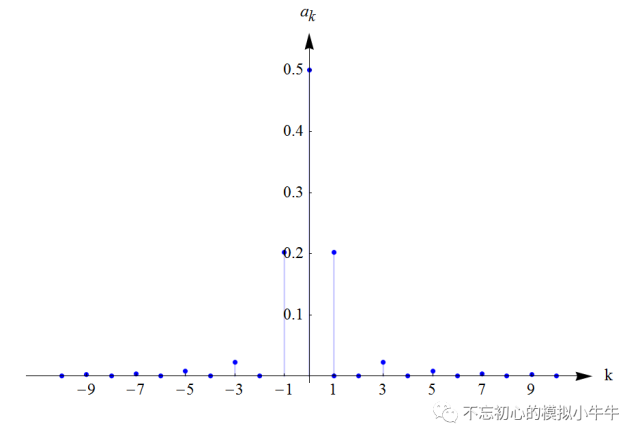
圖6
圖5中例子，當k=0~7時，在一個周期上，傅里葉級數(shù)的直流分量和余弦函數(shù)表示如圖6所示。
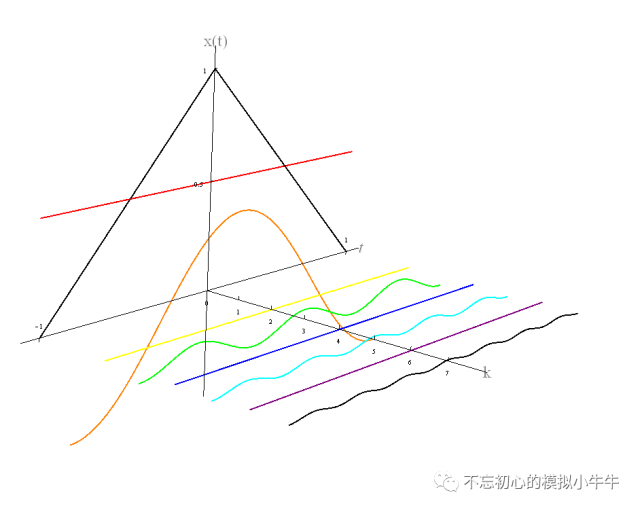
圖7
圖8給出了當k逐漸增大時，有限k項的級數(shù)和的逼近情況。
圖8
一個例子怎么能行，課本上有周期方波的傅里葉級數(shù)展開，這里再給一個臺階信號及其傅里葉級數(shù)逼近的過程。其中藍色為周期等于1的臺階信號，在t=0.25，0.75和1處存在不連續(xù)點。紅色為當k增大時，有限k項傅里葉級數(shù)表示的信號，灰色是紅色在t-x(t)平面的投影。可以看到“吉伯斯現(xiàn)象”(Gibbs phenomenon)。在間斷點處出現(xiàn)過沖和振蕩。
圖9
當然，不是時域的任意信號都能夠表示的傅里葉級數(shù)都是收斂的。需要滿足一定的條件。對于傅里葉級數(shù)的收斂條件，德國數(shù)學家，狄利克雷(Dirichlet，1805~1859）于1829年發(fā)表了任意函數(shù)展開為傅里葉級數(shù)及收斂性的文章。也成為判斷傅里葉級數(shù)收斂的重要條件。
圖10先出"信號"與"系統(tǒng)"的匯總關(guān)系圖。在時域我們基本能完成信號與系統(tǒng)的所有操作。那么通過積分變換，轉(zhuǎn)換到s域或z域。會有與時域不一樣的新特性，和運算的便利性。
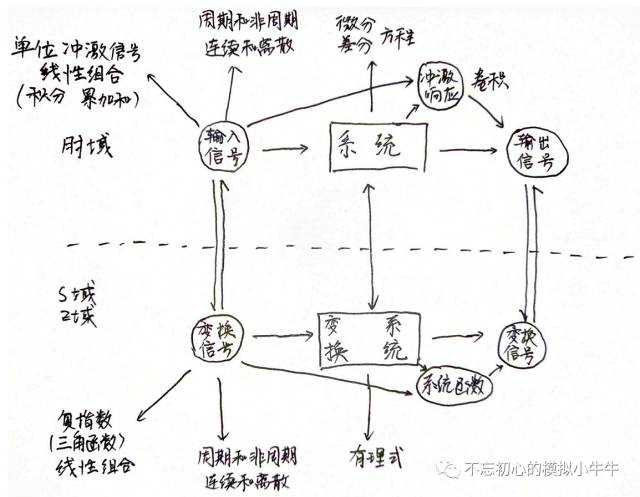
圖10
