還記得計算機網絡中的信道復用技術么? 來來來, 一起復習一下.
why
問: 什么是信道復用. 在回答這個問題之前先看這樣一個場景:
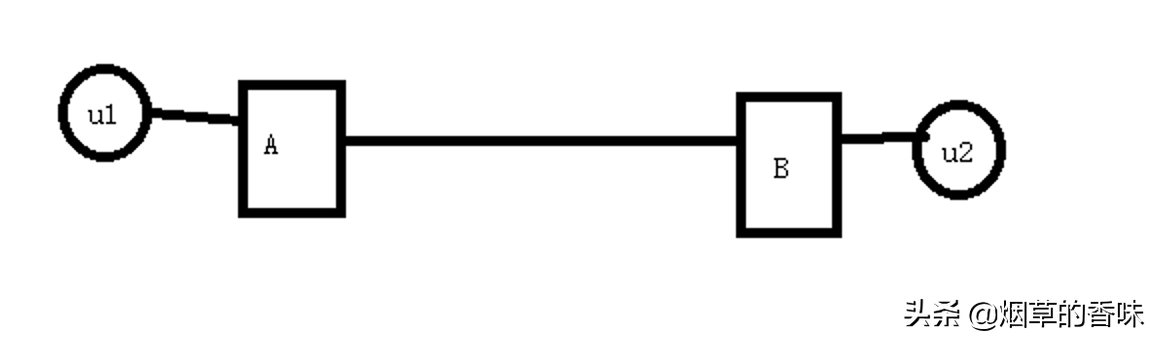
其中u1 u2是兩個用戶, 如果這兩個用戶之間連通的信道在他們使用過程中, 被他們完全占用了, 其他人就只能等著了. 那有人說了, 那就多架設信道不就好了. 如果說 A B之間的信道可以滿足20G 流量的傳輸, 而u1 u2 在通信的過程中, 只使用了其中的千分之一, 這就造成了資源的極度浪費, 不管從哪方面考慮, 都應該充分利用其傳輸的性能.
而這個時候, 為了解決這個問題, 就出現了信道的復用技術. 簡單說, 就是可以在同一個信道上同時傳送多路數據. 如圖:
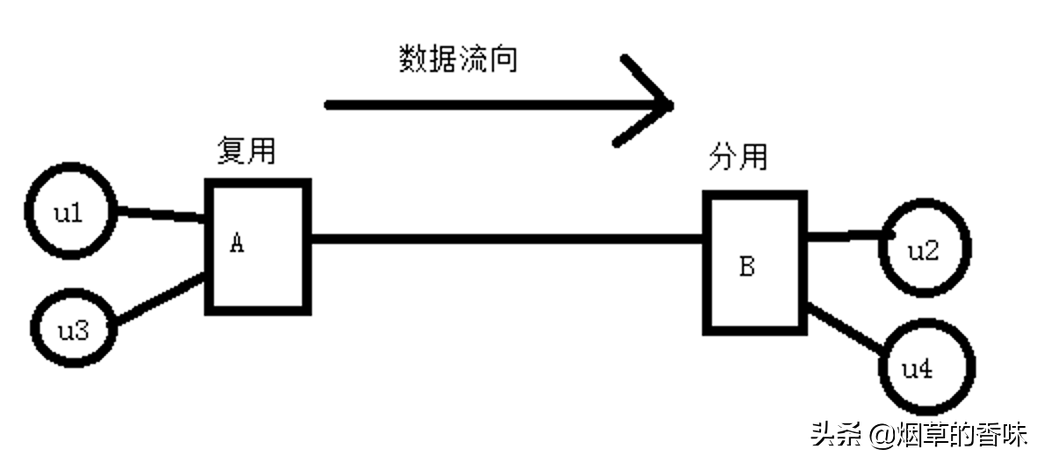
為了方便理解, 將信道轉化為單工通信. 其中u1給u2發送數據的同時, u3也可以給u4發送數據. 同一個信道可傳輸多路信號的通信.
信道復用的基本思路簡單說就是, 在發送端將多路信號揉成一個信號發送, 而接收端需要將信號再拆分成各路信號進行分發.
如何實現信道的復用呢?
頻分復用
現在最常使用的傳輸媒介就是光纖了, 都知道光信號有不同的頻率, 可見光只占用其中的一小部分.
而頻分復用, 就是通過將不同頻率的信號進行融合, 然后在接收端再進行不同頻率信號的分離. 當然, 疊加后的頻率是不能超出傳輸媒介的頻率帶寬的.
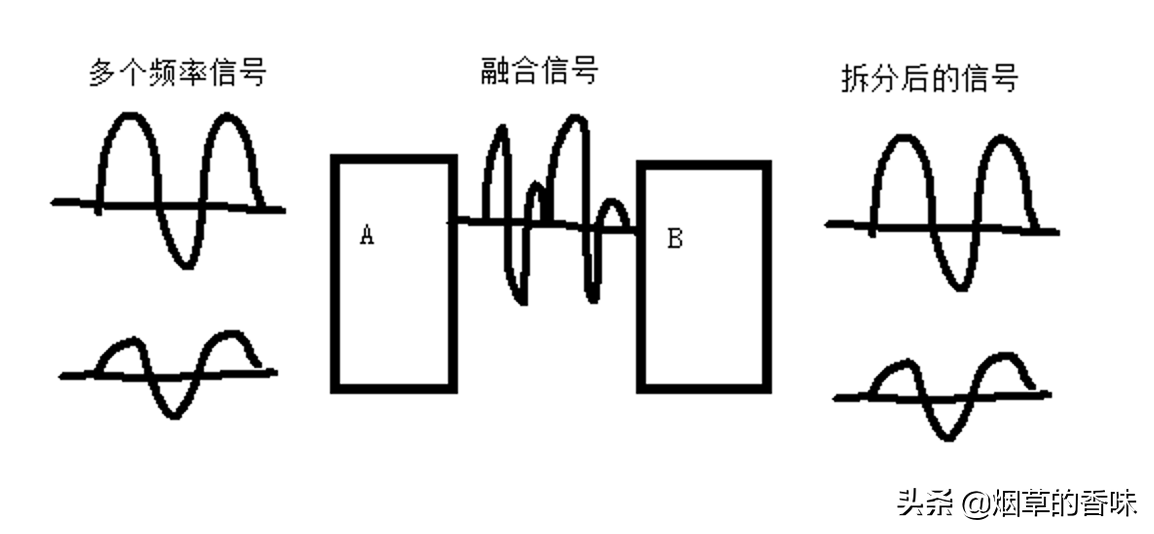
復用技術是可以連續復用的, 從A通過復用, 生成的信號可以在B處再次進行信號的疊加, 而遇到頻率帶寬低的信道可拆分傳輸, 最大限度的使用其傳輸性能.
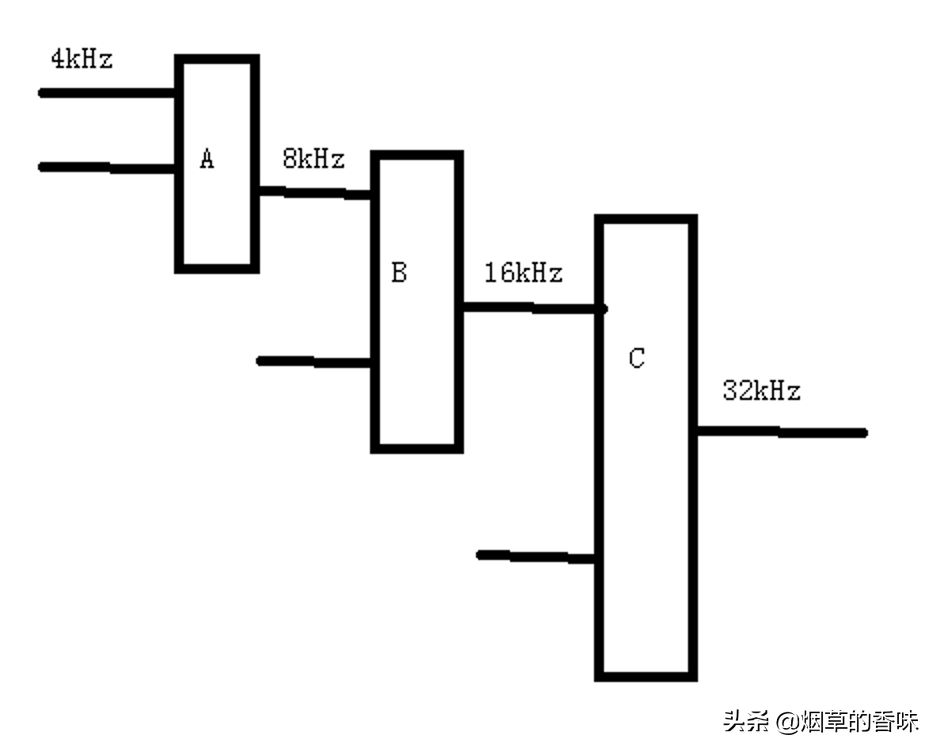
時分復用
時分復用很好理解, 將信道按照時間段進行劃分, 多個輸入端輪流發送數據, 接收端再按照時間段將數據進行拆分.

問題
時分復用技術的問題顯而易見, 每個輸入方占用信道的機會都是均等的. 如果說A沒有數據, 為了接收端能夠按照時間間隔正確分發數據, A所占用的時間間隔會留空, 造成資源的浪費.
統計時分復用
為了解決時分復用空閑造成的資源浪費, 出現了統計時分復用. 基本思路一致, 也是將信道按照時間間隔進行分割, 不同的是, 每次放入數據的時候, 會攜帶一個tag, 標記本段數據的所屬, 接收端根據tag對分段數據進行識別分發(當然, 接收端同時會將附帶的tag去掉). 這樣一來, 只要有數據就方, 而不用空出空閑間隔了.
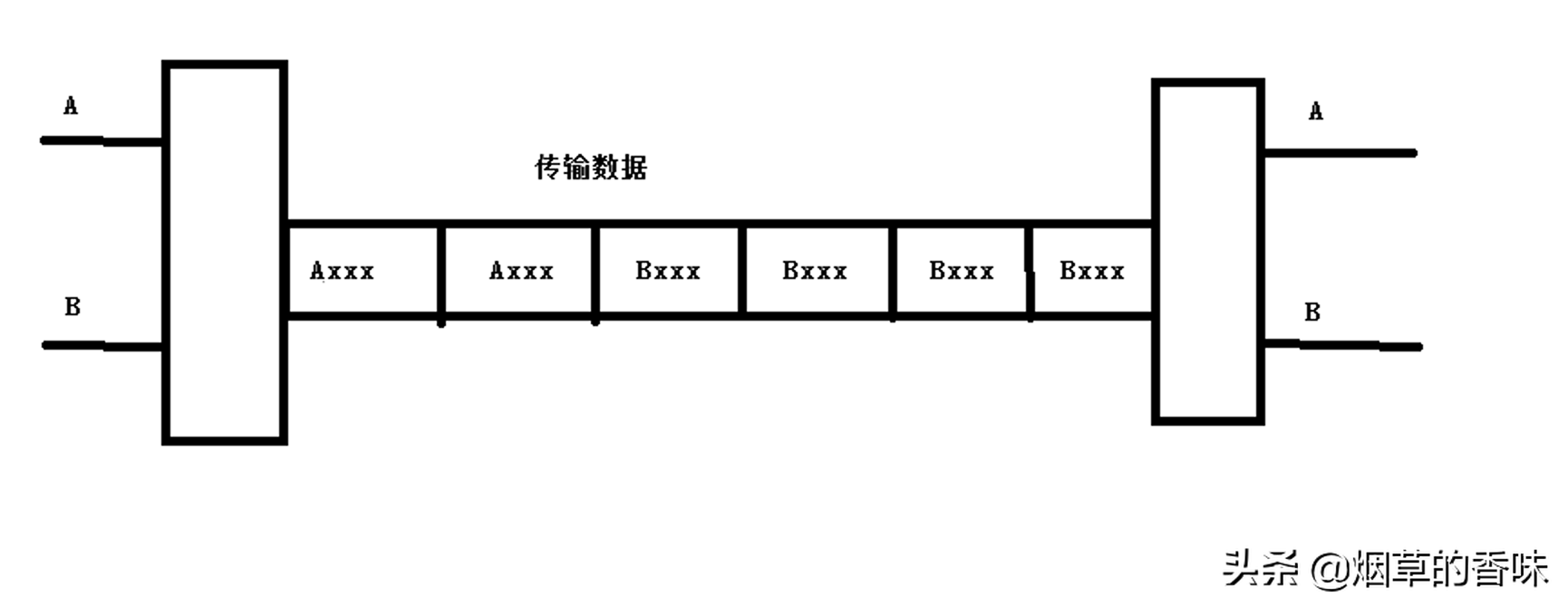
波分復用
波分復用技術說白了, 其實就是頻分復用. 都知道, 光是有不同的波長的, 波分復用是根據不同的波長進行復用.
問題是, 光的波長和頻率成反比, 波長一定, 頻率就也定了. 這這這, 不就是頻分復用換了個名嘛. (可能只是因為在復用時用到的技術不同吧)
碼分復用
先說一下, 碼分復用中的碼是什么. 在傳輸過程中, 將一個比特的時間間隔, 再次切分為 n 個間隔, 其中每個間隔稱為一個碼片.
每個發送接收方, 定義一個自己的碼片序列, 如下:

一共7個碼片(也就是說, 原來發送1比特的數據, 現在需要發送7比特). 當發送數據的時候, 如果是二進制1, 就直接發送碼片序列, 如果是二進制0, 則將碼片序列取反再發送.
那么這個發送的序列如何疊加呢? 很簡單, 就是兩者波形的疊加. 1+1=2, (-1)+(-1)=-2, -1+1=0. (向量的點積) 疊加后的波形是兩個波形的和.
到這里都很好理解, 問題是接收方如何從數據中將波形分離出來呢? 前面的分離都是物理模型, 咱也不太懂, 到這里是數學模型了, 可以簡單嘮一嘮.
先復習一下向量相關的概念
首先, 上方的碼片就是一個包含: 1, -1 的向量.
碼片向量的規格化內積: 按位相乘, 取平均值. (內積是向量的概念, 就是點積除以 n)
根據這個定義, 有如下推理:
- 任一碼片與自身規格化內積為1 (每位都相同, 相乘后均為1, 取平均值任為1)
- 任一碼片與其反碼片內積為-1 (每位都相反, 相乘后均為-1, 取平均值-1)
正交碼片: 內積為0
信號拆分
首先, 容易分離的不同向量必須是正交向量. 證明過程就不說了, 咱也不懂
如何拆分信號呢? 結果很簡單, 將收到的信號與自己的碼片序列做內積運算, 若內積為0, 則當前比特沒有自己的信號, 否則為1或-1, 既1或0.
其他
信道復用技術除了上面幾種, 還有: 空分復用等等.
不同的復用技術, 其對應的應用場景不同. 簡單回顧一下.






