算法算法

從1950年代的早期研究開(kāi)始，機(jī)器學(xué)習(xí)的所有工作似乎都隨著神經(jīng)網(wǎng)絡(luò)的創(chuàng)建而積累起來(lái)。 從邏輯回歸到支持向量機(jī)，相繼提出了新算法之后的算法，但是從字面上看，神經(jīng)網(wǎng)絡(luò)是算法算法和機(jī)器學(xué)習(xí)的頂峰。 它是什么是機(jī)器學(xué)習(xí)的普遍概括，而不是一種嘗試。

從這個(gè)意義上講，它不僅僅是一個(gè)算法，而不僅僅是一個(gè)框架和一個(gè)概念，考慮到構(gòu)建神經(jīng)網(wǎng)絡(luò)的大量自由性，這是顯而易見(jiàn)的-隱藏層和節(jié)點(diǎn)數(shù)，激活函數(shù)，優(yōu)化器，損失函數(shù)，網(wǎng)絡(luò)類型（ 卷積，遞歸等）和專用層（批處理規(guī)范，輟學(xué)等），僅舉幾例。

從這個(gè)角度來(lái)看，神經(jīng)網(wǎng)絡(luò)是一個(gè)概念，而不是一個(gè)嚴(yán)格的算法，這帶來(lái)了一個(gè)非常有趣的推論：任何機(jī)器學(xué)習(xí)算法，無(wú)論是決策樹(shù)還是k近鄰，都可以使用神經(jīng)網(wǎng)絡(luò)來(lái)表示。 雖然本能地通過(guò)幾個(gè)示例可以理解，但是該陳述可以在數(shù)學(xué)上得到證明。

首先讓我們定義一個(gè)神經(jīng)網(wǎng)絡(luò)：它是一個(gè)由輸入層，隱藏層和輸出層組成的體系結(jié)構(gòu)，每一層的節(jié)點(diǎn)之間都有連接。 信息通過(guò)線性變換（權(quán)重和偏差）從非線性層（激活函數(shù)）從輸入層轉(zhuǎn)換為輸出層。 有一些方法可以更新模型的可訓(xùn)練參數(shù)，例如…

Logistic回歸簡(jiǎn)單定義為標(biāo)準(zhǔn)回歸，每個(gè)輸入均具有乘法系數(shù)，并添加了附加截距，所有截距均通過(guò)S型函數(shù)傳遞。 這可以通過(guò)沒(méi)有隱藏層的神經(jīng)網(wǎng)絡(luò)來(lái)建模。 結(jié)果是通過(guò)S形輸出神經(jīng)元的多元回歸。

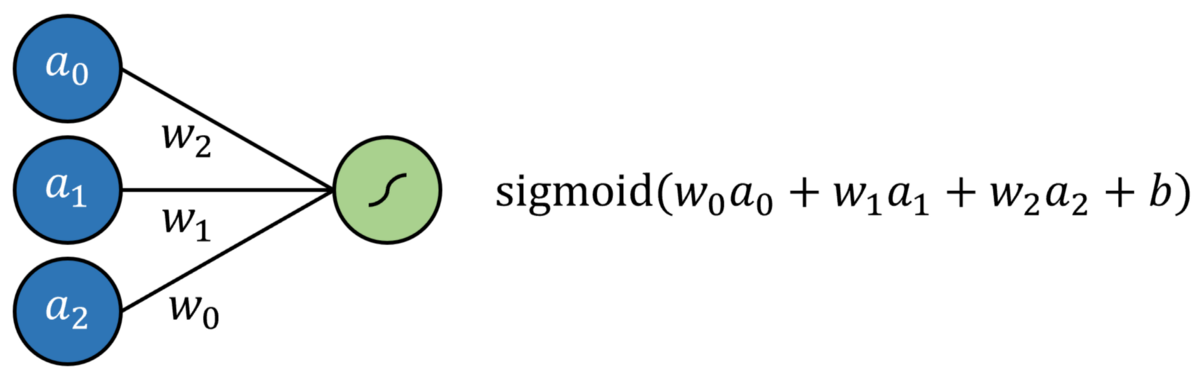
通過(guò)將輸出神經(jīng)元激活函數(shù)替換為線性激活函數(shù)（可以簡(jiǎn)單地映射輸出f（x）= x，換句話說(shuō)，它什么都不做），可以對(duì)線性回歸進(jìn)行建模。

支持向量機(jī)（SVM）算法嘗試通過(guò)所謂的"內(nèi)核技巧"將數(shù)據(jù)投影到新空間中，從而優(yōu)化數(shù)據(jù)的線性可分離性。 轉(zhuǎn)換完數(shù)據(jù)后，該算法將繪制最能沿類邊界將數(shù)據(jù)分開(kāi)的超平面。 超平面被簡(jiǎn)單地定義為現(xiàn)有維度的線性組合，非常像2維的直線和3維的平面。從這個(gè)意義上講，人們可以將SVM算法看作是數(shù)據(jù)到新空間的投影，然后是 多重回歸。 神經(jīng)網(wǎng)絡(luò)的輸出可以通過(guò)某種有界輸出函數(shù)傳遞，以實(shí)現(xiàn)概率結(jié)果。

當(dāng)然，可能需要實(shí)施一些限制，例如限制節(jié)點(diǎn)之間的連接并固定某些參數(shù)，這些更改當(dāng)然不會(huì)脫離"神經(jīng)網(wǎng)絡(luò)"標(biāo)簽的完整性。 也許需要添加更多的層，以確保支持向量機(jī)的這種表現(xiàn)能夠達(dá)到與實(shí)際交易一樣的效果。

諸如決策樹(shù)算法之類的基于樹(shù)的算法有些棘手。 關(guān)于如何構(gòu)建這種神經(jīng)網(wǎng)絡(luò)的答案在于分析它如何劃分其特征空間。 當(dāng)訓(xùn)練點(diǎn)遍歷一系列拆分節(jié)點(diǎn)時(shí)，特征空間將拆分為多個(gè)超立方體。 在二維示例中，垂直線和水平線創(chuàng)建了正方形。

> Source: DataCamp community. Image free to share.

因此，可以通過(guò)更嚴(yán)格的激活來(lái)模擬沿特征線分割特征空間的類似方式，例如階躍函數(shù)，其中輸入是一個(gè)值或另一個(gè)值-本質(zhì)上是分隔線。 權(quán)重和偏差可能需要實(shí)施值限制，因此僅用于通過(guò)拉伸，收縮和定位來(lái)定向分隔線。 為了獲得概率結(jié)果，可以通過(guò)激活函數(shù)傳遞結(jié)果。

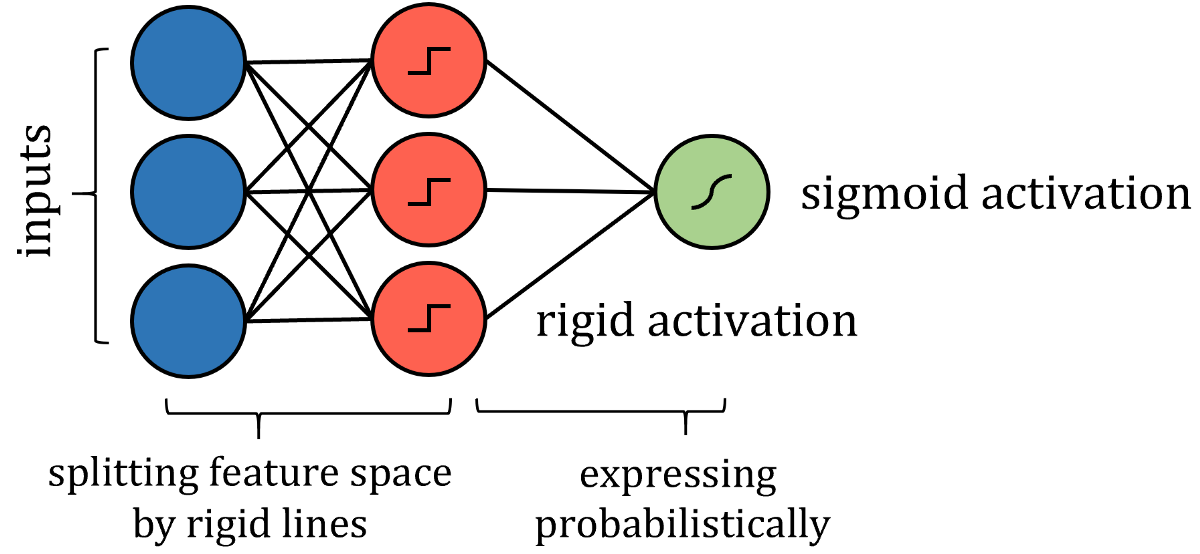
盡管算法的神經(jīng)網(wǎng)絡(luò)表示與實(shí)際算法之間存在許多技術(shù)差異，但重點(diǎn)是網(wǎng)絡(luò)表達(dá)的思想相同，并且可以以與實(shí)際算法相同的策略和性能來(lái)解決問(wèn)題。

但是，也許您不滿意將算法粗略地轉(zhuǎn)換為神經(jīng)網(wǎng)絡(luò)形式，或者希望看到通用的應(yīng)用程序甚至更棘手的算法，例如k近鄰算法或樸素貝葉斯算法，而不是逐案解決。 答案就在于普遍近似定理-神經(jīng)網(wǎng)絡(luò)大獲成功的數(shù)學(xué)解釋-本質(zhì)上說(shuō)，足夠大的神經(jīng)網(wǎng)絡(luò)可以以任意精度對(duì)任何函數(shù)建模。 假設(shè)有一些函數(shù)f（x）代表數(shù)據(jù)； 對(duì)于每個(gè)數(shù)據(jù)點(diǎn)（x，y），f（x）始終返回等于或非常接近y的值。

建模的目的是找到該代表性或真理函數(shù)f（x），我們將其表示為預(yù)測(cè)的p（x）。 所有機(jī)器學(xué)習(xí)算法對(duì)這個(gè)任務(wù)的處理方式都大不相同，將不同的假設(shè)視為有效，并給出其最佳結(jié)果p（x）。 如果要寫出算法創(chuàng)建p（x）的方式，您可能會(huì)從條件列表到純粹的數(shù)學(xué)運(yùn)算中得到任何東西。 描述函數(shù)如何將目標(biāo)映射到輸入的函數(shù)實(shí)際上可以采用任何形式。

有時(shí)，這些功能起作用。 在其他時(shí)候，它們卻沒(méi)有—它們具有固定數(shù)量的參數(shù)，使用或保留它是一件重要的事情。 但是，神經(jīng)網(wǎng)絡(luò)在尋找f（x）的方式上有些不同。

任何函數(shù)都可以由許多類似階梯的部分合理地逼近-步數(shù)越多，逼近的精度就越高。

這些步驟中的每一個(gè)都在神經(jīng)網(wǎng)絡(luò)中表示，即隱層中具有S型激活函數(shù)的節(jié)點(diǎn)，該函數(shù)本質(zhì)上是概率階躍函數(shù)。 本質(zhì)上，每個(gè)節(jié)點(diǎn)都"分配"給函數(shù)f（x）的一部分。 然后，通過(guò)權(quán)重和偏差系統(tǒng)，網(wǎng)絡(luò)可以確定節(jié)點(diǎn)的存在，如果需要為特定輸入激活神經(jīng)元，則將S型函數(shù)的輸入向無(wú)窮大（輸出為1），否則向負(fù)無(wú)窮大。 。 不僅在數(shù)值數(shù)據(jù)中而且在圖像中也觀察到了這種委托節(jié)點(diǎn)以尋找數(shù)據(jù)功能的特定部分的模式。

盡管通用逼近定理已擴(kuò)展為適用于其他激活函數(shù)（如ReLU和神經(jīng)網(wǎng)絡(luò)類型），但原理仍然適用：神經(jīng)網(wǎng)絡(luò)的創(chuàng)建是完美的。 神經(jīng)網(wǎng)絡(luò)不再依賴于復(fù)雜的方程和關(guān)系數(shù)學(xué)系統(tǒng)，而是將自身的一部分委派給數(shù)據(jù)功能的一部分，并通過(guò)蠻力記憶將其歸納在其指定區(qū)域內(nèi)。 當(dāng)這些節(jié)點(diǎn)被聚集到一個(gè)龐大的神經(jīng)網(wǎng)絡(luò)中時(shí)，當(dāng)它們實(shí)際上是巧妙設(shè)計(jì)的近似器時(shí)，結(jié)果是一個(gè)看似智能的模型。

假設(shè)神經(jīng)網(wǎng)絡(luò)至少可以在理論上構(gòu)造出一個(gè)函數(shù)，該函數(shù)基本上具有所需的精度（節(jié)點(diǎn)數(shù)越多，近似值越準(zhǔn)確，當(dāng)然不考慮過(guò)擬合的技術(shù)性），具有正確結(jié)構(gòu)的神經(jīng)網(wǎng)絡(luò)可以 對(duì)任何其他算法的預(yù)測(cè)函數(shù)p（x）建模。 關(guān)于其他任何機(jī)器學(xué)習(xí)算法，都不能這么說(shuō)。

神經(jīng)網(wǎng)絡(luò)使用的方法不是優(yōu)化現(xiàn)有模型中的一些參數(shù)，例如多項(xiàng)式曲線或節(jié)點(diǎn)系統(tǒng)。 神經(jīng)網(wǎng)絡(luò)是對(duì)數(shù)據(jù)建模的某種觀點(diǎn)，其目的不是要充分利用任何獨(dú)立系統(tǒng)，而是要直接逼近數(shù)據(jù)功能。 我們非常熟悉的神經(jīng)網(wǎng)絡(luò)架構(gòu)僅僅是一個(gè)真正想法的模型體現(xiàn)。

借助神經(jīng)網(wǎng)絡(luò)的力量以及對(duì)深度學(xué)習(xí)的無(wú)底領(lǐng)域的不斷研究，無(wú)論是視頻，聲音，流行病學(xué)數(shù)據(jù)還是兩者之間的任何數(shù)據(jù)，都將能夠以前所未有的程度建模。 神經(jīng)網(wǎng)絡(luò)確實(shí)是算法的算法。

除非另有說(shuō)明，否則所有圖片均由作者創(chuàng)建。

(本文翻譯自Matthew P. Burruss的文章《Every machine Learning Algorithm Can Be Represented as a Neural Network》，參考：https://towardsdatascience.com/every-machine-learning-algorithm-can-be-represented-as-a-neural-network-82dcdfb627e3)