一. 近鄰搜索

局部敏感哈希，英文locality-sensetive hashing，常簡稱為LSH。局部敏感哈希在部分中文文獻(xiàn)中也會被稱做位置敏感哈希。LSH是一種哈希算法，最早在1998年由Indyk在上提出。不同于我們在數(shù)據(jù)結(jié)構(gòu)教材中對哈希算法的認(rèn)識，哈希最開始是為了減少沖突方便快速增刪改查，在這里L(fēng)SH恰恰相反，它利用的正式哈希沖突加速檢索，并且效果極其明顯。

LSH主要運(yùn)用到高維海量數(shù)據(jù)的快速近似查找。近似查找便是比較數(shù)據(jù)點(diǎn)之間的距離或者是相似度。因此，很明顯，LSH是向量空間模型下的東西。一切數(shù)據(jù)都是以點(diǎn)或者說以向量的形式表現(xiàn)出來的。在細(xì)說LSH之前必須先提一下K最近鄰查找 (kNN，k-Nearest Neighbor)與c最近鄰查找 (cNN，c-Nearest Neighbor )。 　　 　　kNN問題就不多說了，這個大家應(yīng)該都清楚，在一個點(diǎn)集中尋找距離目標(biāo)點(diǎn)最近的K個點(diǎn)。我們主要提一下cNN問題。首先給出最近鄰查找（NN，Nearest Neighbor）的定義。

定義 1： 給定一擁有n個點(diǎn)的點(diǎn)P，在此集合中尋找距離q 點(diǎn)最近的一個點(diǎn)。

這個定義很容易被理解，需要說明的是這個距離是個廣義的概念，并沒有說一定是歐式距離。隨著需求的不同可以是不同的距離度量手段。那么接下來給出cNN問題的定義。 　　

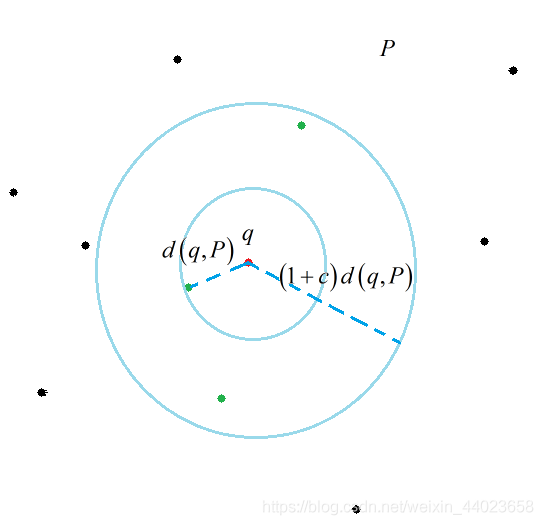
定義 2： 給定一擁有n個點(diǎn)的點(diǎn)集P，在點(diǎn)集中尋找點(diǎn) 這個 滿足 其中d 是P中 距離古點(diǎn)最近一點(diǎn)到的的距離。

cNN不同于kNN，cNN和距離的聯(lián)系更加緊密。LSH本身設(shè)計(jì)出來是專門針對解決cNN問題，而不是kNN問題，但是很多時(shí)候kNN與cNN有著相似的解集。因此LSH也可以運(yùn)用在kNN問題上。這些問題若使用一一匹配的暴力搜索方式會消耗大量的時(shí)間，即使這個時(shí)間復(fù)雜度是線性的。

也許一次兩次遍歷整個數(shù)據(jù)集不會消耗很多時(shí)間，但是如果是以用戶檢索訪問的形式表現(xiàn)出來可以發(fā)現(xiàn)查詢的用戶多了，每個用戶都需要消耗掉一些資源，服務(wù)器往往會承受巨大負(fù)荷。那么即使是線性的復(fù)雜度也是不可以忍受的。早期為了解決這類問題涌現(xiàn)出了許多基于樹形結(jié)構(gòu)的搜索方案，如KD樹，SR樹。但是這些方法只適用于低維數(shù)據(jù)。自從LSH的出現(xiàn)，高維數(shù)據(jù)的近似查找便得到了一定的解決。

二. LSH的定義

LSH不像樹形結(jié)構(gòu)的方法可以得到精確的結(jié)果，LSH所得到的是一個近似的結(jié)果，因?yàn)樵诤芏囝I(lǐng)域中并不需非常高的精確度。即使是近似解，但有時(shí)候這個近似程度幾乎和精準(zhǔn)解一致。 　　 LSH的主要思想是，高維空間的兩點(diǎn)若距離很近，那么設(shè)計(jì)一種哈希函數(shù)對這兩點(diǎn)進(jìn)行哈希值計(jì)算，使得他們哈希值有很大的概率是一樣的。同時(shí)若兩點(diǎn)之間的距離較遠(yuǎn)，他們哈希值相同的概率會很小。給出LSH的定義如下：

定義3： 給定一族哈希函數(shù)H，H是一個從歐式空間S到哈希編碼空間U的映射。如果以下兩個條件都滿足, 則稱此 哈希函數(shù)滿足性。

若則若則

定義3中B表示的是以q為中心， 或 為半徑的空間。其實(shí)還有個版本的定義, 用的是距離的方式, 其實(shí)都是一樣的。（至于說為什么是同時(shí)時(shí)出現(xiàn)，如果要嚴(yán)密的說這確實(shí)是個問題，但是人家大牛的論文下的定義, 不要在意這些細(xì)節(jié) 我繪制了一幅圖來說明一下這個定義。

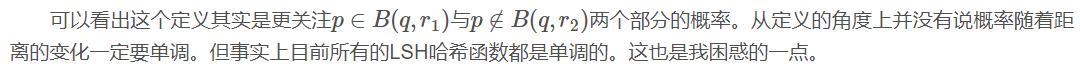
三. 曼哈頓距離轉(zhuǎn)換成漢明距離

從理論講解的邏輯順序上來說，現(xiàn)在還沒到非要講具體哈希函數(shù)的時(shí)候，但是為了方便理解，必須要舉一個實(shí)例來講解會好一些。那么就以曼哈頓距離下（其實(shí)用的是漢明距離的特性）的LSH哈希函數(shù)族作為一個參考的例子講解。 　　曼哈頓距離又稱L1L1范數(shù)距離。其具體定義如下：

定義 4： 在n維歐式空間 中任意兩點(diǎn) 他們之間的買哈頓距離為:

其實(shí)曼哈頓距離我們應(yīng)該并不陌生。他與歐式距離（L2范數(shù)距離）的差別就像直角三角形兩邊之和與斜邊的差別。其實(shí)在這篇論文發(fā)表的時(shí)候歐式距離的哈希函數(shù)還沒有被探究出來，原本LSH的設(shè)計(jì)其實(shí)是想解決歐式距離度量下的近似搜索。所以當(dāng)時(shí)這個事情搞得就很尷尬，然后我們的大牛Indyk等人就強(qiáng)行解釋，大致意思是：不要在意這些細(xì)節(jié)，曼哈頓和歐式距離差不多。他在文章中提出了兩個關(guān)鍵的問題。 　　1.使用L1范數(shù)距離進(jìn)行度量。 　　2.所有坐標(biāo)全部被正整數(shù)化。 　　對于第一條他解釋說L1范數(shù)距離與L2范數(shù)距離在進(jìn)行近似查找時(shí)得到的結(jié)果非常相似。對于第二條，整數(shù)化是為了方便進(jìn)行01編碼。

對數(shù)據(jù)集 所有的點(diǎn), 令C作為所有點(diǎn)中坐標(biāo)的最大值m, 也就是上限。下限是0，這個很明顯。然后就可以把 嵌入漢明空間 其中 此處 是數(shù)據(jù)點(diǎn)在原來歐式空間的維度。對于 個點(diǎn) 如果用 '空間的坐標(biāo)表示就是:

Unary_ 是一串長度為 二進(jìn)制的漢明碼，其意思是前 位為1 后 位為0。舉個例子, C若為5 x 為3，則 Unary=11100 。 是多個 Unary 拼接而成。此時(shí)可以發(fā)現(xiàn)對于兩點(diǎn) 他們之間的曼哈頓距離和通過變換坐標(biāo)后的漢明距 離是一樣的。到此處, 我們可以針對漢明距離來定義一族哈希函數(shù)。

##四. 漢明距離下的LSH哈希函數(shù)

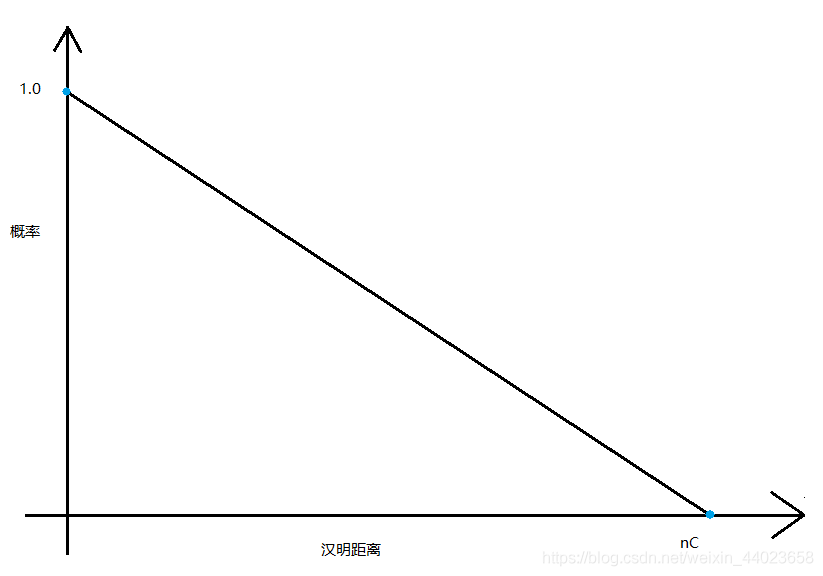
五. LSH的重要參數(shù)

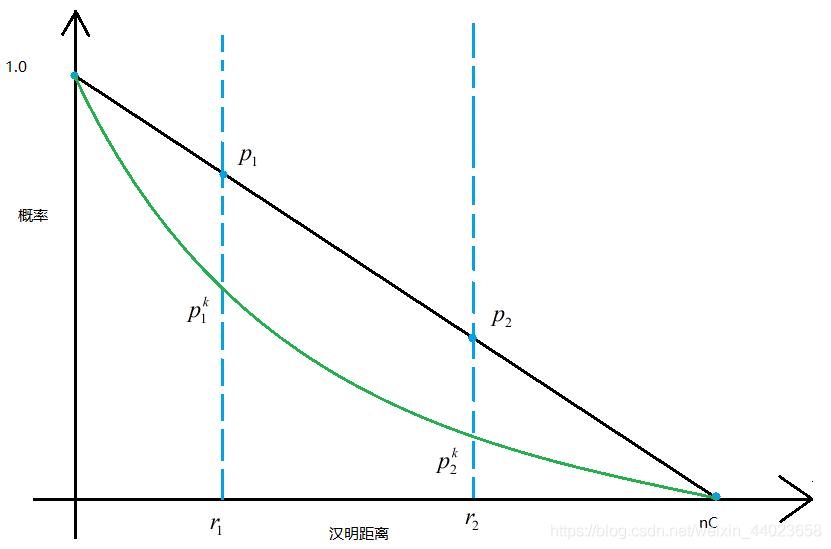
當(dāng)基本哈希函數(shù)確定, 理論上講只要 通過改變 l都可以將 時(shí)的哈希概率差距拉的很大。代價(jià)是要 足夠大的 這也是LSH一個致命的弊病。 說了這么多我們來舉一個實(shí)例幫助理解。

例1：數(shù)據(jù)點(diǎn)集合P由以下6個點(diǎn)構(gòu)成:

可知坐標(biāo)出現(xiàn)的最大值是4，則 維度為2, 則 顯然n 。我們進(jìn)行8位漢明碼編碼。

若我我們現(xiàn)在采用k = 2, l = 3生成哈希函數(shù)。 由 構(gòu)成。每個 由它對應(yīng)的 構(gòu)成
假設(shè)有如下結(jié)果。 分別抽取第2，4位。 分別抽取第1，6位。 分別抽取第3，8位。 哈希表的分布如下圖所示。

可以計(jì)算出 。則分別取出表1,2，3的11，11，11號哈希桶的數(shù)據(jù)點(diǎn)與q比較。依次是C,D,E,F。算出距離q最近的點(diǎn)為F。當(dāng)然這個例子可能效果不是很明顯。原始搜索空間為6個點(diǎn), 現(xiàn)在搜索空間為4個點(diǎn)。對于剛接觸LSH的人會有個疑問。如果不同哈希表的數(shù)據(jù)點(diǎn)重復(fù)了 怎么辦, 會不會增加搜索空間的大小。

首先要說的是這個概率很小, 為什么呢。試想假設(shè)兩個不同哈希表的哈希桶對 查詢有相同點(diǎn), 這意味著在兩張哈希表中這個點(diǎn)與q都有相同哈希值。如果使用單個哈希函數(shù)q和此點(diǎn)被哈希到一起的概率 為 則剛才那個事件發(fā)生的概率為 這個概率是很小的。當(dāng)然也有很多辦法可以解決這個問題。這不是一個大問 題。

我在實(shí)際運(yùn)用時(shí)k大概總是取10-20之間的數(shù), l大致20-100左右。每次對 q進(jìn)行候選點(diǎn)匹配時(shí), 候選的樣本點(diǎn)數(shù)量已 經(jīng)是P的十分之一到百分之一了。就好比P有10000個數(shù)據(jù)點(diǎn), 使用暴力匹配要遍歷整個數(shù)據(jù)集, 使用LSH可能只要匹配1 00到1000個點(diǎn)就可以了。而且往往我都能找到最近點(diǎn)。即使找不到最近的，總體成功率也在90%-98%左右。

之前講解的是一個大致思想，有很多細(xì)節(jié)沒有說明白。 比如哈希表和哈希桶的具體表現(xiàn)形式。就好比我給出的是個邏輯結(jié)構(gòu), 并沒有說清楚它的物理結(jié)構(gòu)。現(xiàn)在說說通常是怎么 具體實(shí)施的。其實(shí)我想說的是物理結(jié)構(gòu)這個東西每個人都可以設(shè)計(jì)一個自己習(xí)慣的，不一定非要按某個標(biāo)準(zhǔn)來。車要的是 思想。 當(dāng)k的數(shù)值很大時(shí), 對于擁有大量數(shù)據(jù)點(diǎn)的 產(chǎn)生不同的哈希值會很多。這種二進(jìn)制的編碼的哈希值最多可以有2 種。這樣一來可能會產(chǎn)生大量哈希桶, 于是平我們可以采用一種方法, 叫二級哈希。首先我們可以將數(shù)據(jù)點(diǎn)p哈希到編碼 為 的哈希桶。

然后我們可以用一個普通的哈希將哈希桶 哈希到一張大小為M 的哈希表中。注意這里的 是針對 哈希桶的數(shù)目而不是針對點(diǎn)的數(shù)量。至于第二個哈希具體這么做, 我想學(xué)過數(shù)據(jù)結(jié)構(gòu)的同學(xué)都應(yīng)該知道。對于哈希桶而 言，我們限制它的大小為 也就是說它最多可以放下 個點(diǎn)。當(dāng)它的點(diǎn)數(shù)量達(dá)到B時(shí), 原本我們可以重新開辟一段空間 放多余的點(diǎn), 但是我不放入, 舍棄它。

假設(shè)點(diǎn)集P有n個點(diǎn), M與B有如下關(guān)系：

是內(nèi)存利用率。對查詢q的近鄰點(diǎn)時(shí)，我們要搜索所有哈希表至少 個點(diǎn)。因此磁盤的訪問是有上界的，上界便是l。 我們現(xiàn)在來分析下l，k的取值問題。首先我們列出兩個事件。 假如我們的哈希函數(shù)是滿足 性的。

P1：如果存在一個點(diǎn) 至少存在一個 滿足

P2： q通過 哈希到的塊中僅包含 以外的點(diǎn)的塊數(shù)小于cl。

定理 則P1,P2可以保證至少 的概率。其中

總結(jié):

以上便是LSH的基本理論, 我總結(jié)一下。對于LSH算的主要流程分為兩個部分，一個是建立哈希結(jié)構(gòu)，另一個便是檢 索。在知道具體度量方式的情況下，利用該度量下的LSH哈希函數(shù)，建立哈希結(jié)構(gòu)。首先選取合適的k，l參數(shù)，然后建立 l張哈希表，每張哈希表用k個獨(dú)立抽取的基本哈希函數(shù)聯(lián)合判斷，建立哈希表的內(nèi)部結(jié)構(gòu)。哈希值相同的點(diǎn)放在一起，哈 希值不同的放在不同的地方。至于查詢，當(dāng)q成為我們的查詢點(diǎn), 首先計(jì)算q在每張哈希表的哈希值，取出對應(yīng)哈希值的哈 希桶內(nèi)所有點(diǎn)，與q做距離計(jì)算。找到滿足我們條件的點(diǎn)作為查詢結(jié)果。

六、局部敏感哈希規(guī)整

說到Hash，大家都很熟悉，是一種典型的Key-Value結(jié)構(gòu)，最常見的算法莫過于MD5。其設(shè)計(jì)思想是使Key集合中的任意關(guān)鍵字能夠盡可能均勻的變換到Value空間中，不同的Key對應(yīng)不同的Value，即使Key值只有輕微變化，Value值也會發(fā)生很大地變化。這樣特性可以作為文件的唯一標(biāo)識，在做下載校驗(yàn)時(shí)我們就使用了這個特性。但是有沒有這樣一種Hash呢？他能夠使相似Key值計(jì)算出的Value值相同或在某種度量下相近呢？甚至得到的Value值能夠保留原始文件的信息，這樣相同或相近的文件能夠以Hash的方式被快速檢索出來，或用作快速的相似性比對。位置敏感哈希（Local Sensitive Hashing, LSH）正好滿足了這種需求，在大規(guī)模數(shù)據(jù)處理中應(yīng)用非常廣泛，例如已下場景：

1. 近似檢測（Near-duplicate detection）：通常運(yùn)用在網(wǎng)頁去重方面。在搜索中往往會遇到內(nèi)容相似的重復(fù)頁面，它們中大多是由于網(wǎng)站之間轉(zhuǎn)載造成的。可以對頁面計(jì)算LSH，通過查找相等或相近的LSH值找到Near-duplicate。
2. 圖像、音頻檢索：通常圖像、音頻文件都比較大，并且比較起來相對麻煩，我們可以事先對其計(jì)算LSH，用作信息指紋，這樣可以給定一個文件的LSH值，快速找到與其相等或相近的圖像和文件。
3. 聚類：將LSH值作為樣本特征，將相同或相近的LSH值的樣本合并在一起作為一個類別。

LSH(Location Sensitive Hash),即位置敏感哈希函數(shù)。與一般哈希函數(shù)不同的是位置敏感性，也就是散列前的相似點(diǎn)經(jīng)過哈希之后，也能夠在一定程度上相似，并且具有一定的概率保證。 LSH的形式化定義可參見前面部分。

如下圖，空間上的點(diǎn)經(jīng)位置敏感哈希函數(shù)散列之后，對于q，其rNN有可能散列到同一個桶（如第一個桶）,即散列到第一個桶的概率較大，會大于某一個概率閾值p1;而其(1+emxilong)rNN之外的對象則不太可能散列到第一個桶，即散列到第一個桶的概率很小，會小于某個閾值p2.

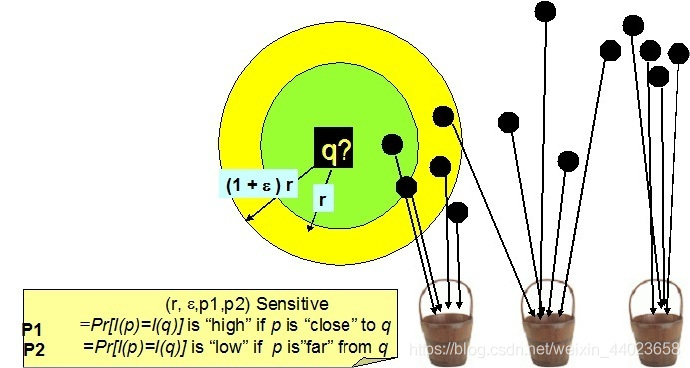
LSH的作用:

◆高維下近似查詢 相似性檢索在各種領(lǐng)域特別是在視頻、音頻、圖像、文本等含有豐富特征信息領(lǐng)域中的應(yīng)用變得越來越重要。豐富的特征信息一般用高維向量表示，由此相似性檢索一般通過K近鄰或近似近鄰查詢來實(shí)現(xiàn)。一個理想的相似性檢索一般需要滿足以下四個條件[4]：

1. 高準(zhǔn)確性。即返回的結(jié)果和線性查找的結(jié)果接近。
2. 空間復(fù)雜度低。即占用內(nèi)存空間少。理想狀態(tài)下，空間復(fù)雜度隨數(shù)據(jù)集呈線性增長，但不會遠(yuǎn)大于數(shù)據(jù)集的大小。
3. 時(shí)間復(fù)雜度低。檢索的時(shí)間復(fù)雜度最好為O（1）或O（logN)。
4. 支持高維度。能夠較靈活地支持高維數(shù)據(jù)的檢索。

此外, 檢索模式應(yīng)能快速地構(gòu)造索引數(shù)據(jù)結(jié)構(gòu), 并且可以完成插入、刪除等操作。

傳統(tǒng)主要方法是基于空間劃分的算法——tree類似算法，如R-tree，Kd-tree，SR-tree。這種算法返回的結(jié)果是精確的，但是這種算法在高維數(shù)據(jù)集上的時(shí)間效率并不高。實(shí)驗(yàn)[5]指出維度高于10之后，基于空間劃分的算法時(shí)間復(fù)雜度反而不如線性查找。LSH方法能夠在保證一定程度上的準(zhǔn)確性的前提下，時(shí)間和空間復(fù)雜度得到降低，并且能夠很好地支持高維數(shù)據(jù)的檢索。

現(xiàn)有的很多檢索算法并不能同時(shí)滿足以上的所有性質(zhì)。以前主要采用基于空間劃分的算法–tree 算法, 例如: R-tree[6], Kd-tree[7],SR-tree。這些算法返回的結(jié)果都是精確的, 然而它們在高維數(shù)據(jù)集上時(shí)間效率并不高。文獻(xiàn)[5]的試驗(yàn)指出在維度高于10之后, 基于空間劃分的算法的時(shí)間復(fù)雜度反而不如線性查找。

1998年, P.Indy和R.Motwani提出了LSH算法的理論基礎(chǔ)。1999 年Gionis A,P.Indy和R.Motwani使用哈希的辦法解決高維數(shù)據(jù)的快速檢索問題, 這也是Basic LSH算法的雛形。2004 年, P.Indy 提出了LSH 算法在歐幾里德空間(2-范數(shù))下的具體解決辦法。同年, 在自然語言處理領(lǐng)域中, Deepak Ravichandran使用二進(jìn)制向量和快速檢索算法改進(jìn)了Basic LSH 算法, 并將其應(yīng)用到大規(guī)模的名詞聚類中, 但改進(jìn)后的算法時(shí)間效率并不理想。

2005 年, Mayank Bawa, Tyson Condie 和Prasanna Ganesan 提出了LSH Forest算法, 該算法使用樹形結(jié)構(gòu)代替哈希表, 具有自我校正參數(shù)的能力。2006 年, R. Panigrahy用產(chǎn)生近鄰查詢點(diǎn)的方法提高LSH 空間效率, 但卻降低了算法的空間效率。2007年,William Josephson 和Zhe Wang使用多重探測的方法改進(jìn)了歐幾里德空間(2-范數(shù))下的LSH 算法, 同時(shí)提高了算法的時(shí)間效率和空間效率。

◆分類和聚類 根據(jù)LSH的特性，即可將相近（相似）的對象散列到同一個桶之中，則可以對圖像、音視頻、文本等豐富的高維數(shù)據(jù)進(jìn)行分類或聚類。

◆數(shù)據(jù)壓縮。如廣泛地應(yīng)用于信號處理及數(shù)據(jù)壓縮等領(lǐng)域的Vector Quantization量子化技術(shù)。 總而言之，哪兒需要近似kNN查詢，哪兒都能用上LSH.

進(jìn)入LSH實(shí)現(xiàn)部分，將按LSH的發(fā)展順序介紹幾種應(yīng)用廣泛的LSH算法。

1, 基于Stable Distribution投影方法 2, 基于隨機(jī)超平面投影的方法; 3, SimHash; 4, Kernel LSH

1, 基于Stable Distribution投影方法

2008年IEEE Signal Process上有一篇文章Locality-Sensitive Hashing for Finding Nearest Neighbors是一篇較為容易理解的基于Stable Dsitrubution的投影方法的Tutorial, 有興趣的可以看一下. 其思想在于高維空間中相近的物體，投影（降維）后也相近。基于Stable Distribution的投影LSH，就是產(chǎn)生滿足Stable Distribution的分布進(jìn)行投影，最后將量化后的投影值作為value輸出. 更詳細(xì)的介紹在Alexandr Andoni維護(hù)的LSH主頁中，理論看起來比較復(fù)雜，不過這就是LSH方法的鼻祖啦，缺點(diǎn)顯而易見：你需要同時(shí)選擇兩個參數(shù)，并且量化后的哈希值是一個整數(shù)而不是bit形式的0和1，你還需要再變換一次。如果要應(yīng)用到實(shí)際中，簡直讓你抓狂。

2, 基于隨機(jī)超平面投影的方法

大神Charikar改進(jìn)了上種方法的缺點(diǎn)，提出了一種隨機(jī)超平面投影LSH. 這種方法的最大優(yōu)點(diǎn)在于：

1),不需要參數(shù)設(shè)定

2),是兩個向量間的cosine距離，非常適合于文本度量

3),計(jì)算后的value值是比特形式的1和0，免去了前面算法的再次變化

3, SimHash

前面介紹的LSH算法，都需要首先將樣本特征映射為特征向量的形式，使得我們需要額外存儲一個映射字典，難免麻煩，大神Charikar又提出了大名鼎鼎的SimHash算法，在滿足隨機(jī)超平面投影LSH特性的同時(shí)避免了額外的映射開銷，非常適合于token形式的特征。 首先來看SimHash的計(jì)算過程： a，將一個f維的向量V初始化為0；f位的二進(jìn)制數(shù)S初始化為0； b，對每一個特征：用傳統(tǒng)的hash算法（究竟是哪種算法并不重要，只要均勻就可以）對該特征產(chǎn)生一個f位的簽名b。對i=1到f： 如果b的第i位為1，則V的第i個元素加上該特征的權(quán)重； 否則，V的第i個元素減去該特征的權(quán)重。 c，如果V的第i個元素大于0，則S的第i位為1，否則為0； d，輸出S作為簽名。

大家引用SimHash的文章通常都標(biāo)為2002年這篇Similarity Estimation Techniques from Rounding Algorithms, 而這篇文章里實(shí)際是討論了兩種metric的hash. 作者猜測, SimHash應(yīng)該是隨機(jī)超平面投影LSH，而不是后來的token形式的SimHash. 其實(shí)只是概念的歸屬問題, 已經(jīng)無關(guān)緊要了

我想很多人引用上篇文章也有部分原因是因?yàn)?7年google研究院的Gurmeet Singh Manku在WWW上的這篇paper: Detecting Near-Duplicates for Web Crawling, 文中給出了simhash在網(wǎng)絡(luò)爬蟲去重工作的應(yīng)用，并利用編碼的重排列方式解決快速Hamming距離搜索問題.

4, Kernel LSH

前面講了三種LSH算法，基本可以解決一般情況下的問題，不過對于某些特定情況還是不行：比如輸入的key值不是均勻分布在整個空間中，可能只是集中在某個小區(qū)域內(nèi)，需要在這個區(qū)域內(nèi)放大距離尺度。又比如我們采用直方圖作為特征，往往會dense一些，向量只分布在大于0的區(qū)域中，不適合采用cosine距離，而stable Distribution投影方法參數(shù)太過敏感，實(shí)際設(shè)計(jì)起來較為困難和易錯，不免讓我們聯(lián)想，是否有RBF kernel這樣的東西能夠方便的縮放距離尺度呢？或是我們想得到別的相似度表示方式。這里就需要更加fancy的kernel LSH了。