
作者 | 蘿卜
來源 | 早起Python/ target=_blank class=infotextkey>Python(ID: zaoqi-python)
用Python基于主成分分析常見的三個應用場景中,其中有一個是「數據描述」,以描述產品情況為例,比如著名的波士頓矩陣,子公司業務發展狀況,區域投資潛力等,需要將多變量壓縮到少數幾個主成分進行描述,壓縮到兩個主成分是最理想的,這樣便可在一張圖內表現出來。
但這類分析一般做主成分分析是不充分的,能夠做到因子分析更好。但因子分析的知識點非常龐雜,所以本文將跳過原理,直接通過案例再次「實戰PCA分析」,用于主成分分析到因子分析的一個過渡,目標有兩個:
-
能夠通過主成分分析結果來估計生成的主成分所表示的含義
-
借以引出因子分析的優勢和學習的必要性是本文的目標
需求說明
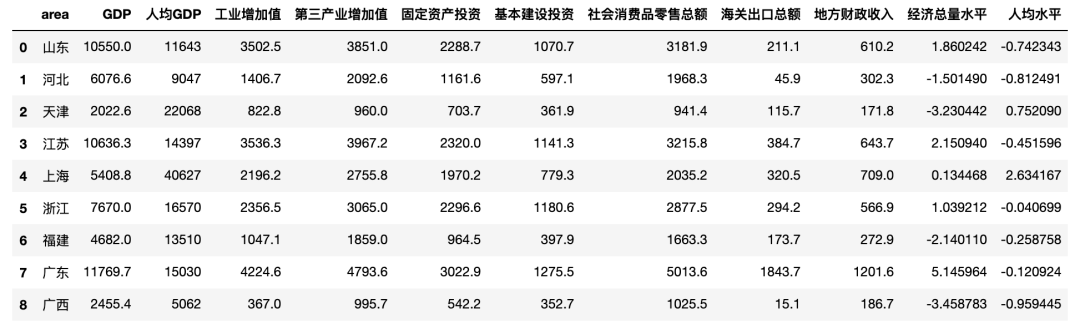
公司希望從事數據分析崗位的你僅用兩個短句就概括出以下數據集所反映出的經濟現象。

用幾個長句都不一定能夠很好的描述數據集的價值,更何況高度凝練的兩個短句,短短九個指標就已經十分讓人頭疼了,如果表格再寬一些呢,比如有二三十個變量?
Python實戰
本節我們將使用Python對上面的數據進行分析。
數據探索
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-whitegrid')
plt.rc('font', **{'family': 'Microsoft YaHei, SimHei'})
# 設置中文字體的支持
plt.rcParams['axes.unicode_minus'] = False
# 解決保存圖像是負號'-'顯示為方塊的問題
sns.set(font='SimHei') # 解決Seaborn中文顯示問題
df = pd.read_csv('城市經濟.csv')
df
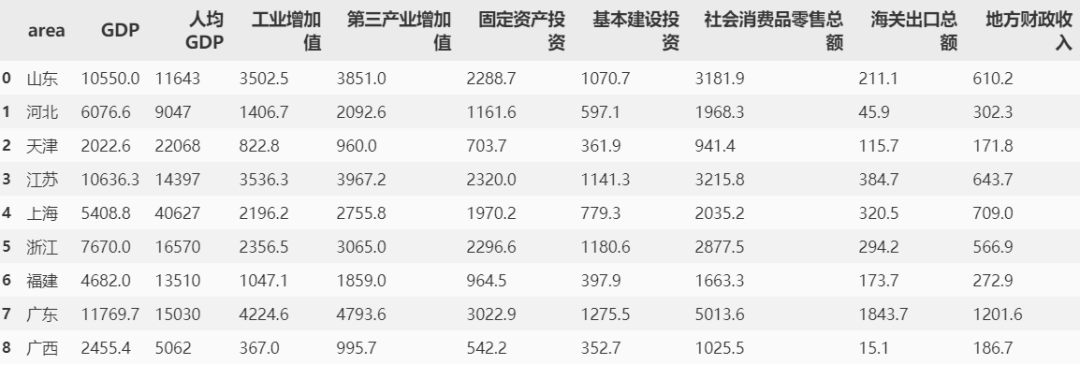
在做主成分分析前,都應該進行變量間相關性的探索,畢竟如果變量是獨立的,則不可壓縮。
plt.figure(figsize=(8, 6))
sns.heatmap(data=df.corr, annot=True) # annot=True: 顯示數字
發現變量間的相關性較高,有變量壓縮的必要性
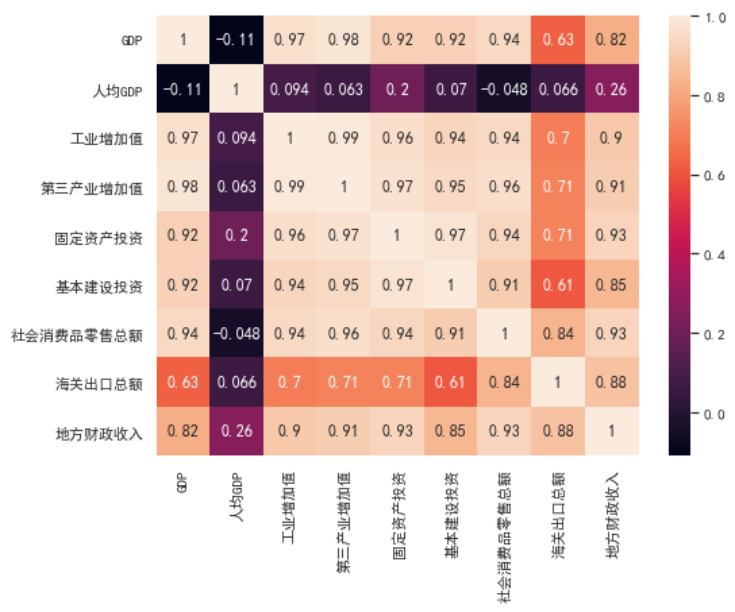
PCA建模
數據標準化
使用中心標準化,即將變量都轉化成z分數的形式,避免量綱問題對壓縮造成影響
from sklearn.preprocessing import scale
data = df.drop(columns='area') # 丟棄無用的類別變量
data = scale(data)
初步建模
需要說明的是第一次的n_components參數最好設置得大一些(保留的主成份),觀察explained_variance_ratio_取值變化,即每個主成分能夠解釋原始數據變異的百分比
from sklearn.decomposition import PCA
pca = PCA(n_components=9) # 直接與變量個數相同的主成分
pca.fit(data)
結果分析
累積解釋變異程度
# 累積解釋變異程度
plt.plot(np.cumsum(pca.explained_variance_ratio_), linewidth=3)
plt.xlabel('成份數')
plt.ylabel('累積解釋方差'); plt.grid(True)
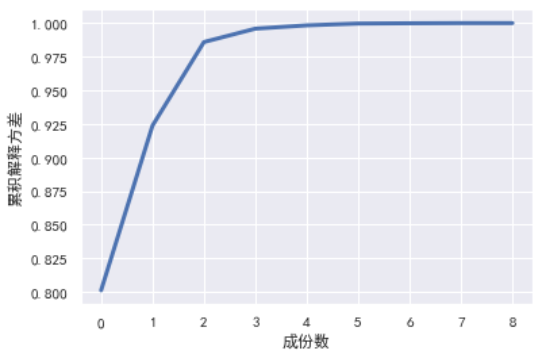
可以看出,當取主成分數為2時,累積解釋方差就已經達到0.97有多(0.85 就已經足夠),說明我們只需要取兩個主成分即可
重新建模
綜上可知兩個主成分就已經足夠了
pca = PCA(n_components=2) # 直接與變量個數相同的主成分
pca.fit(data)
pca.explained_variance_ratio_
new_data = pca.fit_transform(data) # fit_transform 表示將生成降維后的數據
# 查看規模差別
print("原始數據集規模: ", data.shape)
print("降維后的數據集規模:", new_data.shape)

可以看到9個變量壓縮成兩個主成分!
主成分中各變量的權重分析
先看兩個主成分與 9 個變量的系數關系
results = pd.DataFrame(pca.components_).T
results.columns = ['pca_1', 'pca_2']
results.index = df.drop(columns='area').columns
results
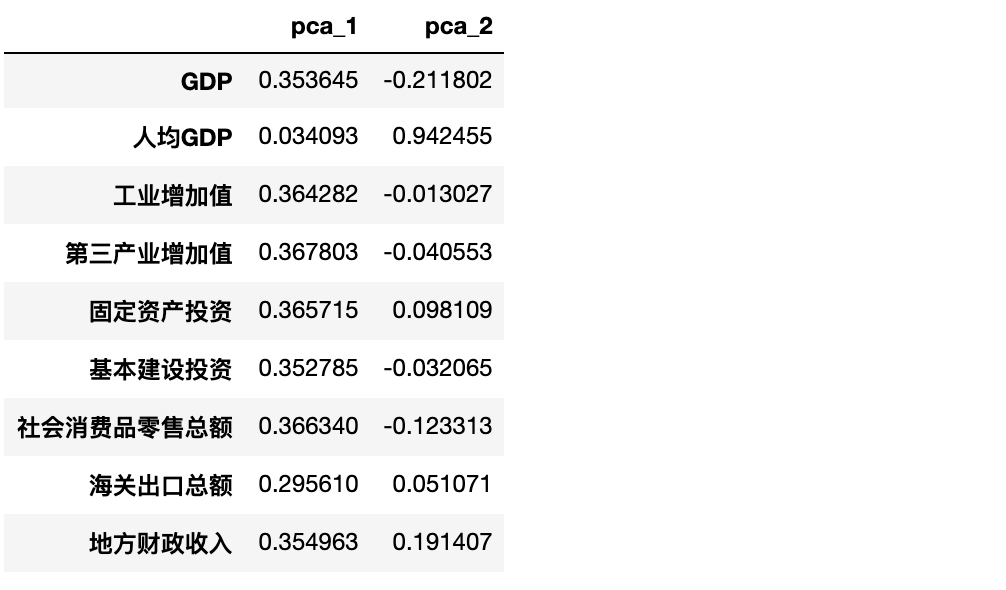
可以明顯看出:
-
主成分1幾乎不受data的第二個自變量
人均GDP的影響,0.034,其他自變量對其影響程度都差不多。 -
主成分2受data的第二個自變量
人均GDP影響最大,達到了0.94
結果描述
通過上面的PCA建模,我們把9個自變量壓縮成了2 主成分,每個主成分受哪些變量的影響也有了了解。雖然得到的主成分都沒有什么意義,但我們是否可以通過變量們對主成分的影響程度來為生成的兩個主成分命名呢?
第一個主成分在表達經濟總量的指標上的權重相當,可考慮命名為經濟總量水平;而第二個主成分只在人均GDP上權重很高,可暫時考慮命名為人均水平
注意:這里的給主成分命名(包括后續有關因子分析的推文)都是對降維后的數據進行的,而不是生成的主成分,這樣才有比較和描述的價值。每個自變量在生成的主成分上的權重只是給這個主成分的命名提供參考,真正的命名操作是對壓縮后的數據進行。
new_data = pca.fit_transform(data) # fit_transform 表示將生成降維后的數據
results = df.join(pd.DataFrame(new_data, # new_data 是降維后的數據
columns=['經濟總量水平', '人均水平'])) # 與原來的數據拼接
results
繪制波士頓矩陣,這里的散點圖的點標注代碼是前人的優秀輪子,直接拿來用即可。
plt.figure(figsize=(10, 8))
# 基礎散點圖
x, y = results['經濟總量水平'], results['人均水平']
label = results['area']
plt.scatter(x, y)
plt.xlabel('經濟總量水平'); plt.ylabel('人均水平')
# 對散點圖中的每一個點進行文字標注
## 固定代碼,無需深究,拿來即用
## 給點標注是需要將 x 和 y 以及標簽如上段代碼那樣單獨拆開
for a,b,l in zip(x,y,label):
plt.text(a, b+0.1, '%s.' % l, ha='center', va='bottom', fontsize=14)
# 添加兩條豎線
plt.vlines(x=results['經濟總量水平'].mean,
ymin=-1.5, ymax=3, colors='red')
plt.hlines(y=results['人均水平'].mean,
xmin=-4, xmax=6, colors='red')
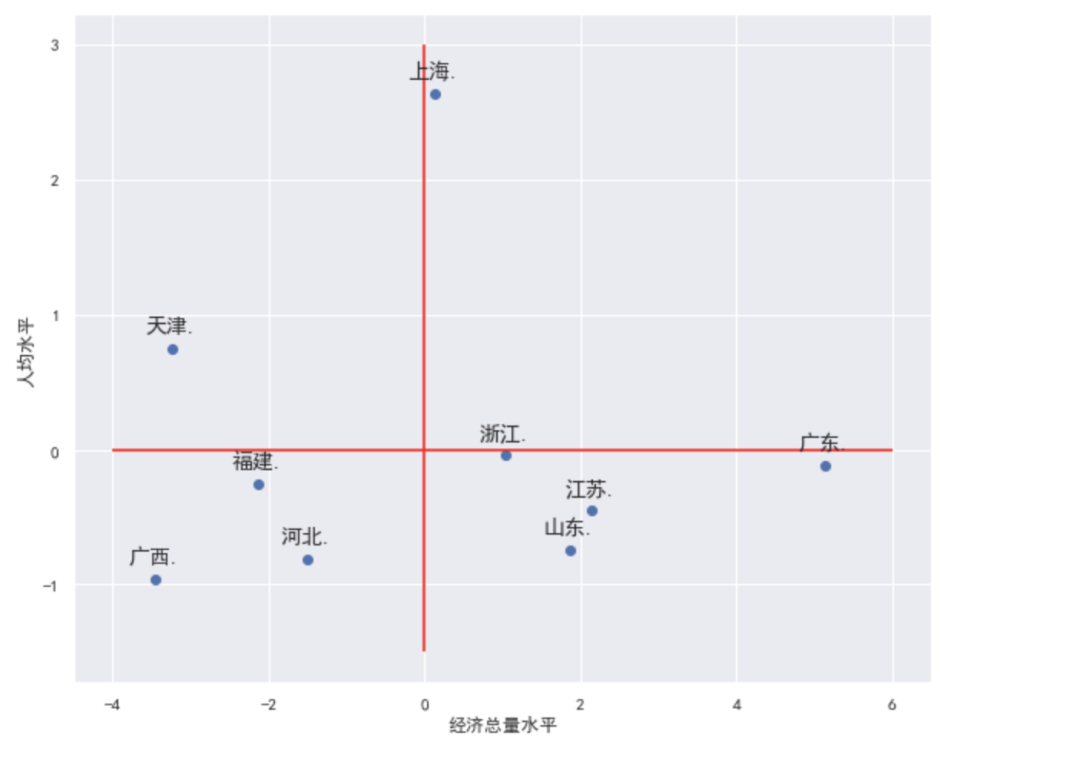
最終從上圖可以看出:
-
廣西,河北,福建三地的人均水平和經濟總量水平都偏低
-
上海的人均經濟水平很高,但經濟總量水平缺只是略優于均值
-
廣東的人均經濟水平稍次于均值,但經濟總量水平很高
-
......
小結
本文講解了基于主成分分析的樣本特征描述,并使用Python示范了完整的流程。其中,也對由多個自變量生成的主成分的命名描述操作中需要注意的點作了比較詳細的說明。其實PCA并不能非常好的滿足維度分析的需求,能夠做到「因子分析」最好,它是主成分方法的拓展,作為維度分析的手段,因子分析也是構造合理的聚類模型和穩健的分類模型的必然步驟。
Python商業數據挖掘自動化系列代碼及數據已經上傳GitHub,如有需要可以自行下載:「https://github.com/liuhuanshuo/zaoqi-Python/tree/master/商業數據分析實戰」。






