作者 | Mr Bear

編輯 | 叢 末

近年來(lái)，隨著圖神經(jīng)網(wǎng)絡(luò)在各個(gè)領(lǐng)域的火熱應(yīng)用，越來(lái)越多的學(xué)者試圖從圖論的角度對(duì)圖神經(jīng)網(wǎng)絡(luò)的表達(dá)能力進(jìn)行理論分析，并基于這些理論分析開(kāi)發(fā)出了性能強(qiáng)大的模型。然而，在實(shí)際應(yīng)用中，這些在理論上非常強(qiáng)大的模型的性能往往會(huì)受到計(jì)算復(fù)雜度等因素的限制。

本文作者 Michael Bronstein 是一名來(lái) 自帝國(guó)理工學(xué)院的教授，同時(shí)也是 Twitter 圖機(jī)器學(xué)習(xí)項(xiàng)目組的負(fù)責(zé)人。在本文中，他深入淺出地介紹了近年來(lái)分析圖神經(jīng)網(wǎng)絡(luò)表達(dá)能力的工作，并介紹了他們對(duì)于該領(lǐng)域未來(lái)發(fā)展方向的思考。

1圖神經(jīng)網(wǎng)絡(luò)和 WL 圖同構(gòu)測(cè)試之間的關(guān)系

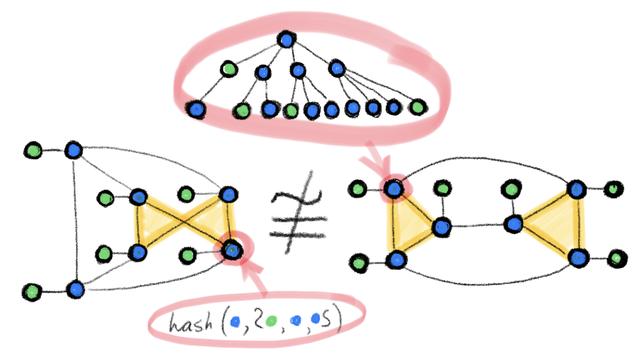
眾所周知，傳統(tǒng)的前饋神經(jīng)網(wǎng)絡(luò)（多層感知機(jī)）是一種通用函數(shù)近似器：它們能夠以任意的準(zhǔn)確率逼近任意的平滑函數(shù)。對(duì)于近期興起的圖神經(jīng)網(wǎng)絡(luò)來(lái)說(shuō)，其表征性質(zhì)還不太為人所知。在實(shí)驗(yàn)中，我們經(jīng)常可以看到圖神經(jīng)網(wǎng)絡(luò)在某些數(shù)據(jù)集上性能優(yōu)異，但同時(shí)又在另一些數(shù)據(jù)集上表現(xiàn)令人失望。

為了探究造成這種現(xiàn)象的根本原因，我們不得不思考一個(gè)問(wèn)題：圖神經(jīng)網(wǎng)絡(luò)究竟有多強(qiáng)大？

在探究這一問(wèn)題的過(guò)程中，我們所面臨的一個(gè)挑戰(zhàn)是：實(shí)際應(yīng)用場(chǎng)景下使用的圖往往是連續(xù)結(jié)構(gòu)和離散結(jié)構(gòu)（節(jié)點(diǎn)、邊特征、連通性）的組合。因此，該問(wèn)題可以被表述為不同的形式。一種可能的形式化定義是：圖神經(jīng)網(wǎng)絡(luò)是否能夠區(qū)分不同類(lèi)型的圖結(jié)構(gòu)。在圖論中，這是一種被稱(chēng)為「圖同構(gòu)問(wèn)題」的經(jīng)典問(wèn)題，旨在判斷兩個(gè)圖在拓?fù)湟饬x上是否等價(jià)。兩個(gè)同構(gòu)的圖擁有相同的連通性，其差別僅僅可能是節(jié)點(diǎn)的排列不同。

稍令人驚訝的是，我們尚不知曉精確的圖同構(gòu)問(wèn)題的復(fù)雜度級(jí)別。該問(wèn)題在多項(xiàng)式時(shí)間內(nèi)不可解，它也不是一個(gè) NP 完全（NPC）問(wèn)題。有時(shí)，我們將其復(fù)雜度稱(chēng)為一種特殊的「GI 級(jí)」（GI class）。

1、Weisfeiler-Lehman 測(cè)試

Boris Weisfeiler 和 Andrey Lehman 于 1968 年發(fā)表的具有開(kāi)創(chuàng)性意義的論文「The reduction of a graph to canonical form and the algebra which Appears therein 」），提出了一種高效的啟發(fā)式算法，我們現(xiàn)在將其稱(chēng)為「WL 測(cè)試」。

最初，人們認(rèn)為 WL 測(cè)試可以在多項(xiàng)式時(shí)間內(nèi)求解圖同構(gòu)問(wèn)題。但一年之后，人們就舉出了一個(gè)反例。然而，從概率意義上說(shuō)，似乎 WL 測(cè)試對(duì)于幾乎所有的圖都有效。

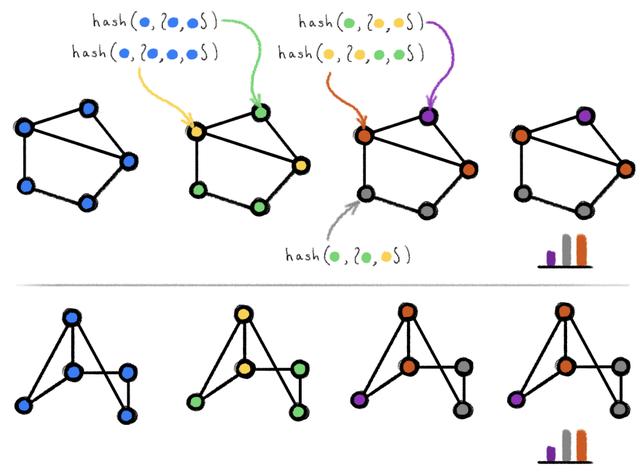
圖 1：在兩個(gè)同構(gòu)圖上執(zhí)行 WL 測(cè)試的示例。包含弧線的 hash 圓括號(hào)代表多重集。在著色情況不再變化后算法會(huì)終止，并給出輸出結(jié)果（顏色直方圖）。若將兩圖輸入給該算法得到的輸出相同，則說(shuō)明兩圖可能同構(gòu)。

WL 測(cè)試是建立在迭代式的圖重著色（圖論中的「著色」指的是一種離散的節(jié)點(diǎn)標(biāo)簽）基礎(chǔ)上的，在初始狀態(tài)下，每個(gè)節(jié)點(diǎn)的顏色均不相同。在每一步迭代中，算法會(huì)聚合節(jié)點(diǎn)及其鄰居節(jié)點(diǎn)的顏色，并將它們表征為多重集，然后將聚合得到的顏色多重集通過(guò) Hash 函數(shù)映射到某種唯一的新顏色上。當(dāng)達(dá)到穩(wěn)定的著色狀態(tài)（各節(jié)點(diǎn)著色狀態(tài)不再變化）后，算法終止。當(dāng)算法終止后，若兩圖的著色情況不同，則我們認(rèn)為它們「非同構(gòu)」。如果兩圖著色情況相同，它們可能（但并不一定）是同構(gòu)的。換句話(huà)說(shuō)，WL 測(cè)試是圖同構(gòu)的必要非充分條件。有一些非同構(gòu)的圖在接受 WL 測(cè)試后得到的著色情況也是相同的，而在這種情況下 WL 測(cè)試就失效了，因此我們只能認(rèn)為它們「可能同構(gòu)」。下圖展示了其中的一種可能性：

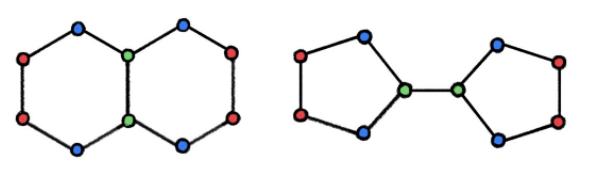
圖 2：顯然，WL 圖同構(gòu)測(cè)試會(huì)為上面的兩個(gè)非同構(gòu)圖生成相同的著色結(jié)果，此時(shí) WL 測(cè)試失效。在化學(xué)領(lǐng)域中，這兩個(gè)圖分別代表兩種不同的化合物「decalin」（左圖）和「bicyclopentyl」（右圖）的分子結(jié)構(gòu)。

2、圖同構(gòu)網(wǎng)絡(luò)（GIN）

Keyulu Xu 等人發(fā)表的論文「 How powerful are graph neural networks?」和 Christopher Morris 等人發(fā)表的論文，以及 Thomas 在他至少兩年前撰寫(xiě)的博客「GRAPH CONVOLUTIONAL NETWORKS」，中注意到，WL 測(cè)試與圖消息傳遞神經(jīng)網(wǎng)絡(luò)有驚人的相似之處，它們都在圖上進(jìn)行了一種類(lèi)似于卷積的操作。

相關(guān)論文/文章鏈接：

https://arxiv.org/abs/1810.00826

https://tkipf.github.io/graph-convolutional-networks/

在一個(gè)消息傳遞層中，每個(gè)節(jié)點(diǎn)的特征會(huì)以聚合其鄰居節(jié)點(diǎn)特征的方式被更新。對(duì)聚合和更新操作的選擇是十分重要的：只有使用多重集的單射函數(shù)才能使其與 WL 算法等價(jià)。在前人的研究中，「取最最大值」或「取均值」等聚合操作都是一定弱于 WL 的能力，它們甚至不能區(qū)分非常簡(jiǎn)單的圖結(jié)構(gòu)：

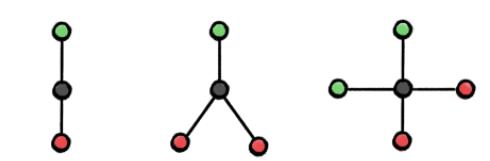
圖 3：通過(guò)「取最大值」操作無(wú)法區(qū)分左圖、中圖、右圖，通過(guò)「取均值」聚合函數(shù)可以區(qū)分左圖和中圖、通過(guò)「取最大值」和「取均值」操作均無(wú)法區(qū)分左圖和右圖。這是因?yàn)橥ㄟ^(guò)這些方法從黑色節(jié)點(diǎn)的鄰居中聚合而來(lái)的特征將會(huì)是相同的。

Xu 提出了一種聚合和更新函數(shù)的選擇方案，它使得消息傳遞神經(jīng)網(wǎng)絡(luò)與 WL 算法等價(jià)，該網(wǎng)絡(luò)被稱(chēng)為「圖同構(gòu)網(wǎng)絡(luò)」（GIN）。該網(wǎng)絡(luò)和標(biāo)準(zhǔn)的消息傳遞神經(jīng)網(wǎng)絡(luò)一樣強(qiáng)大。但是，GIN 不僅僅是一種新的網(wǎng)絡(luò)架構(gòu)，其主要影響在于它通過(guò)一種簡(jiǎn)單的設(shè)定形式化定義了圖神經(jīng)網(wǎng)絡(luò)表達(dá)能力的問(wèn)題，這種設(shè)定與圖論中的經(jīng)典問(wèn)題相關(guān)。該網(wǎng)絡(luò)的思路也啟發(fā)了許多后續(xù)的工作。

3、Weisfeiler-Lehman 層次結(jié)構(gòu)

使用更加強(qiáng)大的圖同構(gòu)測(cè)試，是擴(kuò)展 Xu 和 Morris 等人工作的一個(gè)方向。因此，László Babai 提出了 k-WL 測(cè)試，這是 WL 算法在高階上的擴(kuò)展，它在 k 元組上進(jìn)行操作，而非操作單個(gè)節(jié)點(diǎn)。除了 1-WL 和 2-WL 測(cè)試是等價(jià)的，(k+1)-WL 始終嚴(yán)格強(qiáng)于 k-WL（k≥2），即對(duì)于某些圖而言 k-WL 測(cè)試失效，而 (k+1)-WL 測(cè)試可以成功判定圖是否同構(gòu)，但反之則不然。因此，k-WL 是一種層次結(jié)構(gòu)的或隨著 k 的增大而逐漸更加強(qiáng)大的圖同構(gòu)測(cè)試，有時(shí)被稱(chēng)為「Weisfeiler-Lehman 層次結(jié)構(gòu)」。

我們可以設(shè)計(jì)出遵循 k-WL 測(cè)試的圖神經(jīng)網(wǎng)絡(luò)，這種網(wǎng)絡(luò)是一定比消息傳遞架構(gòu)更加強(qiáng)大的。Morris 等人在論文「 Weisfeiler and Leman go neural: Higher-order graph neural networks 」中提出了第一種這樣的架構(gòu) k-GNN。

相關(guān)論文鏈接：

https://aaai.org/ojs/index.php/AAAI/article/view/4384/4262

傳統(tǒng)的消息傳遞神經(jīng)網(wǎng)絡(luò)和這種高階圖神經(jīng)網(wǎng)絡(luò)之間最關(guān)鍵的區(qū)別在于：由于 k-WL 算法在節(jié)點(diǎn)的 k 元組上進(jìn)行操作，所以這種高階圖神經(jīng)網(wǎng)絡(luò)是非局部的（non-local）。這對(duì)算法的實(shí)現(xiàn)及其計(jì)算復(fù)雜度和存儲(chǔ)復(fù)雜度都有重要的影響：k-GNN 需要