
作者:神奇的程序員K
轉發鏈接:https://mp.weixin.qq.com/s/3B8dZRfbIuktSBeArXlmcQ
前言
我們在頁面上渲染數據時,通常會根據特定規則來對數據進行一個排序,然后再將其渲染到頁面展示給用戶。哪么對數據進行排序有很多種方式,哪一種效率高?哪一種穩定性好?那一種占用內存小?本文將詳解經典的八大排序算法以及三種搜索算法,并用TypeScript將其實現,歡迎各位對上述問題迷惑的開發者閱讀本文。
排序算法
我們先來學習下排序算法,八大排序包括:冒泡排序、選擇排序、插入排序、歸并排序、快速排序、計數排序、同排序、基數排序其中有幾個排序我在之前的文章中已經講解了其圖解實現,本文將注重講解其實現,另外幾篇文章鏈接如下:
- 排序算法:冒泡排序
- 排序算法:選擇排序
- 排序算法:插入排序
- 排序算法:歸并排序
- 排序算法:快速排序
冒泡排序
冒泡排序是排序算法中最簡單、最好理解的一個排序算法,但是從運行時間的角度來看,它的效率是最低的。本文中所有函數實現的代碼地址: Sort.ts
實現思路
它會比較相鄰的兩個項,如果第一個比第二個大,則交換它們。元素項向上移動至正確的順序。為了讓排序算法更靈活,不僅僅只是用于數字的排序,因此本文中講解的排序算法都會有一個比對函數作為參數傳進來,用于定義兩個值的比較方式。
- 聲明一個函數其接受兩個參數:待排序數組 & 比對函數
- 第一層循環i:從待排序數組的0號元素開始遍歷數組,遍歷到最后一位,用于控制數組需要經過多少輪排序
- 第二層循環j:從數組的0號元素開始遍歷,遍歷至數組的倒數第二位元素再減去第一層循環i。
- 比較大小,在第二層循環中,將當前遍歷到的元素和其下一個元素比較大小,如果 j > j + 1就交換兩個元素的位置。
我們通過一個例子來描述下上述思路,如下圖所示,將一個亂序數組執行冒泡排序后,將其從小到大排列。
實現代碼
為了讓函數便于維護,我們新建一個類名為Sort,本文中實現的所有函數都為這個類內部的方法。
- 為了函數的可擴展性,我們需要實現一個默認的比對函數,此比對函數作用于本文中的所有排序方法
export function defaultCompare<T>(a: T, b: T): number {
if (a === b) {
return Compare.EQUALS;
} else if (a > b) {
return Compare.BIGGER_THAN;
} else {
return Compare.LESS_THAN;
}
}
// 枚舉類:定義比對返回值
export enum Compare {
LESS_THAN = -1,
BIGGER_THAN = 1,
EQUALS = 0
}
- 在類中聲明需要的變量,并在構造器中聲明需要傳的參數類型,此處適用于本文實現的所有函數
/**
* 排序算法
* @param array 需要進行排序的數組
* @param compareFn 比對函數
*/
constructor(private array: T[] = [], private compareFn: ICompareFunction<T> = defaultCompare) {}
- 實現冒泡排序
// 冒泡排序
bubbleSort(): void {
// 獲取數組長度
const { length } = this.array;
for (let i = 0; i < length; i++) {
// 從數組的0號元素遍歷到數組的倒數第2號元素,然后減去外層已經遍歷的輪數
for (let j = 0; j < length - 1 - i; j++) {
// 如果j > j + 1位置的元素就交換他們兩個元素的位置
if (this.compareFn(this.array[j], this.array[j + 1]) === Compare.BIGGER_THAN) {
this.swap(this.array, j, j + 1);
}
}
}
}
編寫測試代碼
我們將上圖中的例子放在代碼中,測試下執行結果是否正確。
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
sort.bubbleSort();
console.log(array.join());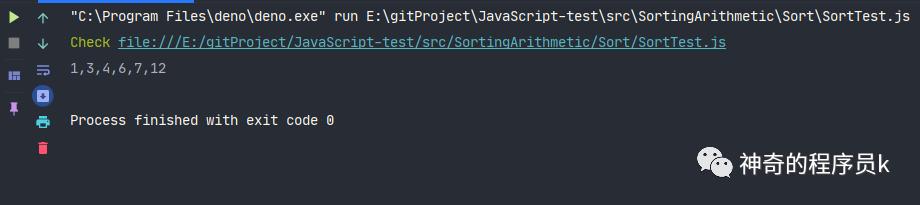
選擇排序
選擇排序是一種原址比較排序算法,它的大致思路是找到數據結構中的最小值并將其放置在第一位,接著找到第二小的值將其放在第二位,依次類推。
實現思路
- 聲明一個輔助變量:indexMin用于存儲數組中的最小值
- 第一層循環i,從數組的0號元素遍歷到數組的倒數第二位。indexMin默認賦值為i,用于控制輪數
- 第二層循環j,從數組的i號元素遍歷到數組的末尾,用于尋找數組的最小值,如果indexMin位置的元素大于j號位置的元素就覆蓋indxMin的值為j
- 在第二層循環結束后,比較i與indexMin是否相等,如果不相等就交換兩個元素的位置。
下圖中的示例描述了上述思路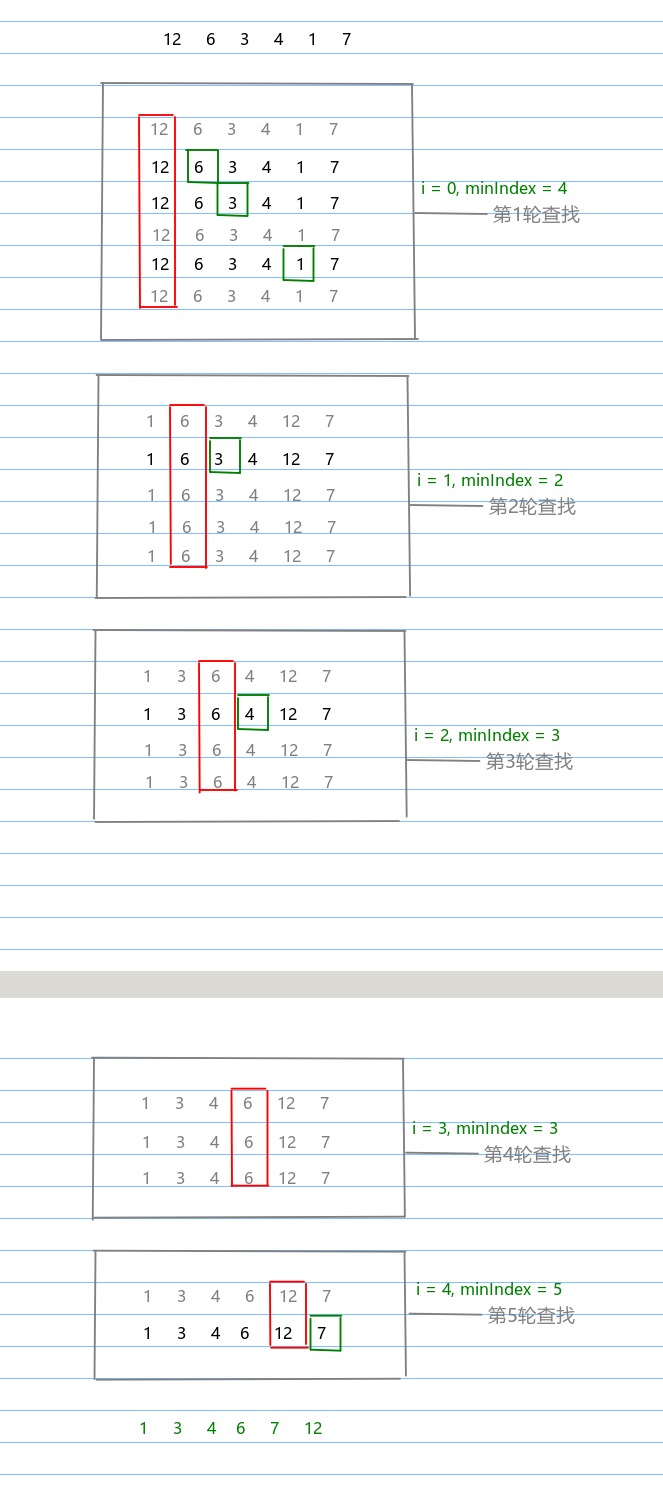
實現代碼
// 選擇排序
selectionSort(): void {
const { length } = this.array;
// 聲明一個變量用于存儲最小元素的位置
let indexMin = 0;
for (let i = 0; i < length; i++) {
// 初始值為外層循環當前遍歷到的位置i
indexMin = i;
for (let j = i; j < length; j++) {
// 如果當前遍歷到元素小于indexMin位置的元素,就將當前遍歷到的位置j賦值給indexMin
if (this.compareFn(this.array[indexMin], this.array[j]) === Compare.BIGGER_THAN) {
indexMin = j;
}
}
if (i !== indexMin) {
this.swap(this.array, i, indexMin);
}
}
}
編寫測試代碼
我們將圖中的示例,放在代碼中,測試排序函數是否都正確執行。
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
// const result = sort.radixSort(array);
// console.log(result.join());
sort.selectionSort();
console.log(array.join());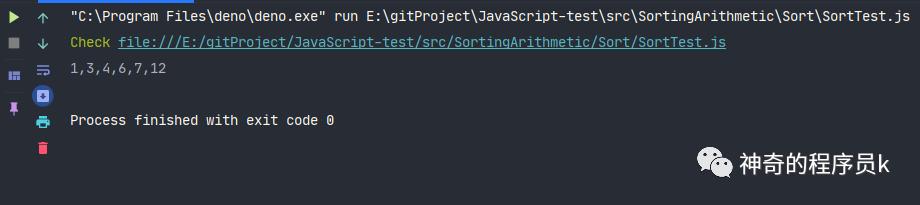
插入排序
插入排序會將數組分為已排序區域和未排序區域,將未排序區域的數組項和已排序區域的數組進行大小比較,確立要插入的位置,然后將其插入到對應的位置。
實現思路
- 第一層循環i:從數組的1號元素開始,遍歷到數組末尾,因為我們會先假設0號元素已經排好序,所以從1號元素開始。
- 用一個臨時變量temp存儲當前i號位置的元素,用一個變量j存儲i
- while循環: j > 0且j - 1位置的元素大于temp,就把j位置的值設置為j - 1 位置的值,最后j--,繼續下一輪遍歷。
- while循環結束后,將temp放到正確的位置array[ j ]
如下圖所示,我們通過一個例子描述了上述插入排序的過程

實現代碼
接下來我們將上述思路轉換為代碼。
// 插入排序
insertionSort(array: T[] = this.array): void {
const { length } = array;
let temp;
// 假設0號元素已經排好序,從1號元素開始遍歷數組
for (let i = 1; i < length; i++) {
// 聲明輔助變量存儲當前i的位置以及其對應的值
let j = i;
temp = array[i];
// j大于0且j-1位置的元素大于i號位置的元素就把j-1處的值移動到j處,最后j--
while (j > 0 && this.compareFn(array[j - 1], temp) === Compare.BIGGER_THAN) {
array[j] = array[j - 1];
j--;
}
// 將temp放到正確的位置
array[j] = temp;
}
}
編寫測試代碼
我們將圖中的例子放在代碼里,執行下查看排序函數是否正常運行。
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
sort.insertionSort(array);
console.log(array.join());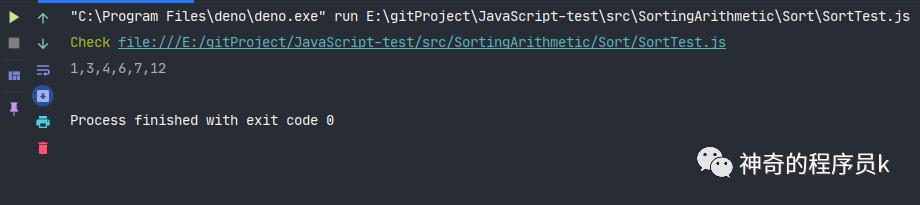
歸并排序
歸并排序是一個可以實際使用的排序算法,在JAVAScript中Array類定義了一個Sort函數,用以排序JavaScript數組。ECMScript沒有定義用哪個排序算法,所以瀏覽器廠商可以自己去實現算法。谷歌瀏覽器的V8引擎使用快速排序實現,火狐瀏覽器使用歸并排序實現。
實現思路
歸并排序是一個分而治之算法,就是將原始數組切分成比較小的數組,直到每個小數組只有一個位置,接著將小數組歸并成比較大的數組,直到最后只有一個排序完畢的大數組。由于是分治法,歸并排序也是遞歸的。我們要將算法分為兩個函數:一個用于將函數分割成小數組,一個用于將小數組合并成大數組。我們先來看看主函數,將數組分割成小數組。
- 遞歸終止條件:由于是遞歸,所以我們需要先設立遞歸終止條件,當數組的長度大于1時就進行歸并排序。
- 獲取數組的中間值: 我們通過數組的中間值來切割數組,將其分成左、右兩部分。對左右兩部分繼續執行分割
- 合并數組: 我們將數組分割完后,對小數組進行排序,然后將其合并成大數組并返回。
接下來,我們再來看下合并函數的實現
- 合并函數接收兩個參數:左、右數組
- 聲明三個輔助變量: i, j, result,分別表示左、右數組的指針以及存儲合并后的數組
- 如果i < left.length && j < right.length,代表指針數組尚未排序完,因此執行下述邏輯
- 如果lef[i] < right[j],就往result中放left[i]的值隨后i++,否則就放right[j]的值隨后j++
- 最后,將left或right數組的剩余項添加進result中
下圖用一個例子描述了上述歸并排序的過程
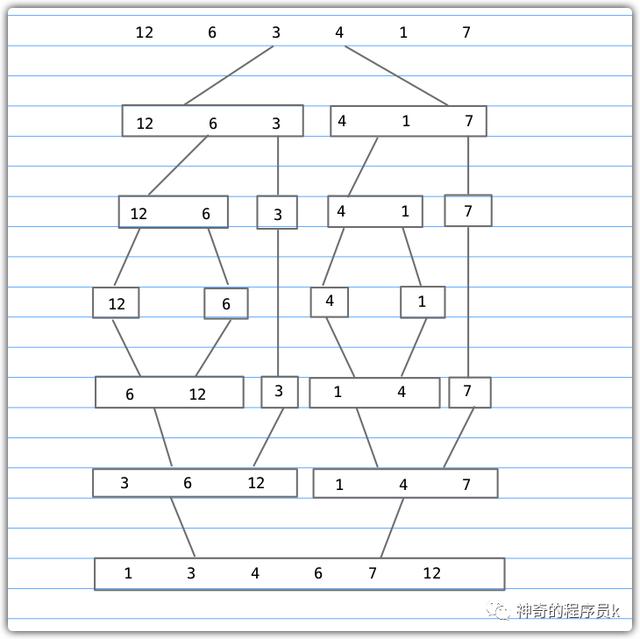
實現代碼
接下來,我們將上述思路轉換為代碼。
// 歸并排序
mergeSort(array: T[] = this.array): T[] {
if (array.length > 1) {
const { length } = array;
// 獲取中間值
const middle = Math.floor(length / 2);
// 遞歸填充左右數組
const left = this.mergeSort(array.slice(0, middle));
const right = this.mergeSort(array.slice(middle, length));
// 合并左右數組
array = this.merge(left, right);
}
return array;
}
private merge(left: T[], right: T[]) {
let i = 0;
let j = 0;
const result: T[] = [];
while (i < left.length && j < right.length) {
// 如果left[i] < right[j]將left[i]加進result中,隨后i自增,否則把right[j]加進result中,隨后j自增
result.push(this.compareFn(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++]);
}
// 將left或right數組的剩余項添加進result中
return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}
編寫測試代碼
我們將上圖中的例子放到代碼中執行用以驗證我們的函數是否正確執行
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
const result = sort.mergeSort();
console.log(result.join());
快速排序
快速排序與歸并排序一樣都是可用作實際應用的算法,它也是使用分而治之的方法,將原始數組分為較小的數組,但它沒有像歸并排序那樣將他們分割開。
實現思路
我們需要三個函數:主函數、排序函數、切分函數。
- 主函數(quickSort),調用排序函數,返回排序函數最終排好的數組。
- 排序函數(quick),接收3個參數: 待排序數組(array)、數組的左邊界(left)、數組的右邊界(right)
- 聲明一個輔助變量index,用于存儲分割子數組的的位置。
- 確立遞歸終止條件:array < 1 ,如果array.length > 1,就執行下述操作:
執行劃分函數,計算劃分點,將得到的值賦值給index;
如果left > index - 1,代表子數組中存在較小值的元素,從數組的left邊界到index-1邊界遞歸執行排序函數;
如果index < right,代表子數組存在較大值的元素,從數組的index到right邊界遞歸執行排序函數;
- 劃分函數(partition),與排序函數一樣,它也接收3個參數。
- 從數組中選擇一個主元pivot,選擇數組的中間值
- 聲明兩個指針:i, j,分別指向左邊數組的第一個值和右邊數組的第一個值。
- 如果i <= j,則代表left指針和right指針沒有相互交錯,則執行下述劃分操作:
移動left指針直至找到一個比主元大的元素,即array[i] > pivot;
移動right指針直至找到一個比主元小的元素,即array[j] < pivot;
當左指針指向的元素比主元大且右指針指向的元素比主元小,并且左指針索引沒有右指針索引大時就交換i號和j號元素的位置,隨后移動兩個指針;
最后,劃分結束,返回i的值;
實現代碼
接下來我們將上述思路轉換為代碼:
/**
*
* @param array 待排序數組
* @param left 左邊界
* @param right 右邊界
* @private
*/
private quick(array: T[], left: number, right: number) {
// 該變量用于將子數組分離為較小值數組和較大值數組
let index;
if (array.length > 1) {
// 對給定子數組執行劃分操作,得到正確的index
index = this.partition(array, left, right);
// 如果子數組存在較小值的元素,則對該數組重復這個過程
if (left < index - 1) {
this.quick(array, left, index - 1);
}
// 如果子數組存在較大值的元素,也對該數組重復這個過程
if (index < right) {
this.quick(array, index, right);
}
}
return array;
}
// 劃分函數
private partition(array: T[], left: number, right: number): number {
// 從數組中選擇一個值做主元,此處選擇數組的中間值
const pivot = array[Math.floor((right + left) / 2)];
// 創建數組引用,分別指向左邊數組的第一個值和右邊數組的第一個值
let i = left;
let j = right;
// left指針和right指針沒有相互交錯,就執行劃分操作
while (i <= j) {
// 移動left指針直至找到一個比主元大的元素
while (this.compareFn(array[i], pivot) === Compare.LESS_THAN) {
i++;
}
// 移動right指針直至找到一個比主元小的元素
while (this.compareFn(array[j], pivot) === Compare.BIGGER_THAN) {
j--;
}
// 當左指針指向的元素比主元大且右指針指向的元素比主元小,并且左指針索引沒有右指針索引大時就交換i和j號元素的位置,隨后移動兩個指針
if (i <= j) {
this.swap(array, i, j);
i++;
j--;
}
}
// 劃分結束,返回左指針索引
return i;
}
編寫測試代碼
我們通過一個例子,來測試下上述代碼是否都正確執行。
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
const result = sort.quickSort();
console.log(result.join());
計數排序
計數排序是一個分布式排序,它是用來排序整數的優秀算法。分布式排序使用已組織好的輔助數據結構,然后進行合并,得到排好序的數組。計數排序使用一個用來存儲每個元素在原始數組中出現次數的臨時數組。在所有元素都計數完成后,臨時數組已排好序并可迭代以構建排序后的結果數組。
實現思路
- 找到要排序數組的最大值
- 以上一步找到的最大值+1為長度創建一個計數數組
- 遍歷要排序的數組,以當前遍歷的元素為索引,尋找計數數組中對應的位置將其初始化為0,如果此處位置有相同元素的話就自增
- 遍歷計數數組,判斷當前遍歷到的元素是否大于0,如果大于0就取當前遍歷到的索引,替換待排序數組中的元素
接下來我們通過一個例子來講解下上述過程,如下圖所示:
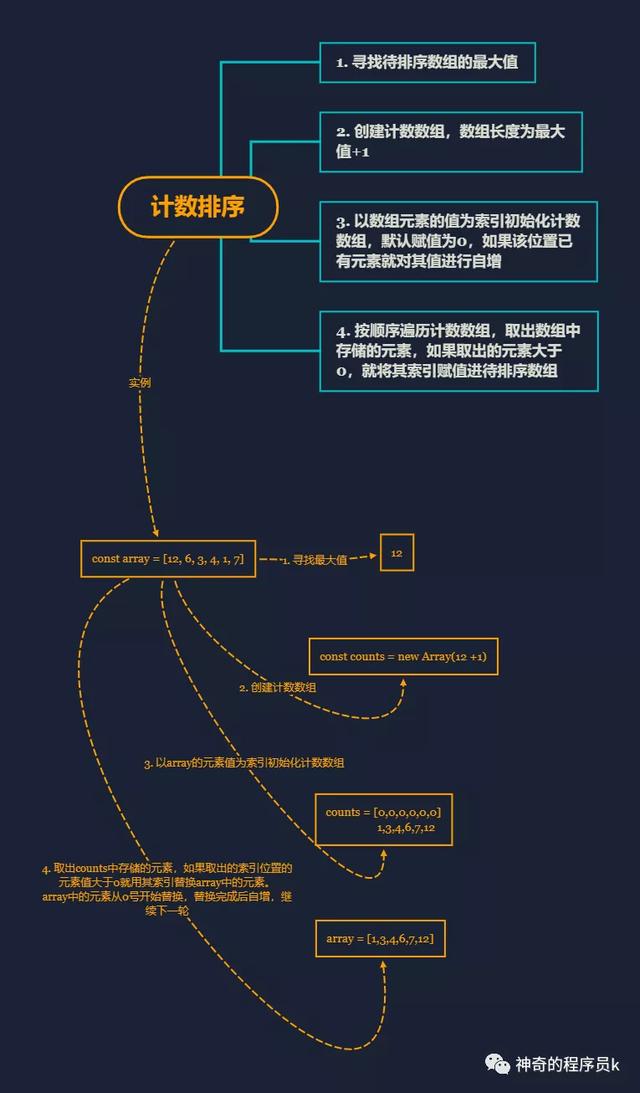
實現代碼
接下來我們將上述思路轉換為代碼
countingSort(array: number[]): number[] {
// 待排序數組為空或只有一個元素則不用排序
if (array.length < 2) {
return array;
}
// 找到待排序數組中的最大值
const maxValue = this.findMaxValue(array);
// 創建計數數組,數組長度為待排序數組的最大值+1
const counts = new Array(maxValue + 1);
// 遍歷待排序數組,為計數數組賦值
array.forEach((element) => {
// 以當前遍歷到的元素值為索引將對應位置元素值初始化為0
if (!counts[element]) {
counts[element] = 0;
}
// 當前位置的值進行自增,順便應對數組中有重復值的情況,有重復值時當前位置的值必定大于1
counts[element]++;
});
// 聲明一個變量用于數組最終排序
let sortedIndex = 0;
// 遍歷計數數組,根據計數數組的元素位置對待排序數組進行排序
counts.forEach((count, i) => {
// 如果當前遍歷到的元素值大于0,則執行替換操作進行排序
while (count > 0) {
// 將當前元素索引賦值給array的sortedIndex號元素,隨后sortedIndex自增
array[sortedIndex++] = i;
// 當前元素值自減,如果其值大于1,證明此處有重復元素,那么我們就繼續執行while循環
count--;
}
});
// 最后,排序完成,返回排序好的數組
return array;
}
編寫測試代碼
我們將上述圖中的例子放進代碼中執行,看看我們寫的函數是否正確執行。
const array = [12, 6, 3, 4, 1, 7];
const sort = new Sort(array);
const result = sort.countingSort(array);
console.log(result.join());
桶排序
桶排序也是一種分布式排序算法,它將元素分為不同的桶,再使用一個簡單的排序算法,例如插入排序,來對每個桶進行排序,最后,它將所有的桶合并為結果數組。
實現思路
首先,我們需要指定需要多個桶來排序各個元素,默認情況,我們會使用5個桶。桶排序在所有元素平分到各個桶中時的表現最好。如果元素非常稀疏,則使用更多的桶會更好。如果元素非常密集,則使用較少的桶會更好。因此我們為了算法的效率,會讓調用者根據實際需求將桶的數量作為參數傳進來。我們將算法分為兩個部分:
- 創建桶,并將桶分布到不同的桶中
- 對每個桶中的元素執行排序算法并將所有桶合并成排序好后的結果數組
我們先來看看創建桶的思路
- 聲明創建桶函數(createBuckets),接收兩個參數:待排序數組(array),桶大小(bucketSize)
- 計算array中的最大值(maxValue)和最小值(minValue)
- 計算每個需要的桶數量,公式為:(maxValue - minValue) / bucketSize)+1
- 聲明一個二維數組buckets,用于存放所有桶
- 根據桶數量,初始化每個桶
- 遍歷array,將每個元素分布到桶中
- 計算需要將元素放到哪個桶中(bucketIndex),公式為:(array[i] - minValue) / bucketSize
- 將元素與放進合適的桶中,即buckets[bucketIndex].push(array[i])
- 將桶返回
接下來我們來看看對每個桶里的元素進行排序的思路
- 創建排序桶函數(sortBuckets),接收一個參數: 桶buckets
- 需要一個輔助數組sortedArray,用于存放排序好的結果數組
- 遍歷sortedArray
- 如果當前桶內存儲的桶buckets[i]不為null,就對其執行插入排序
- 將排序好的桶buckets[i]解構后放進sortedArray中
- 最后,返回sortedArray
我們通過一個例子,來講解上述思路,如下圖所示
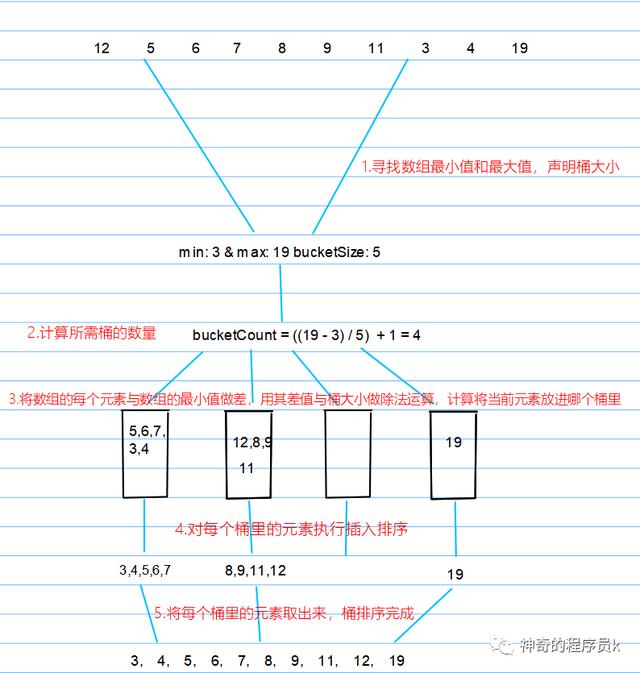
實現代碼
接下來,我們將上述思路轉換為代碼。
// 桶排序
bucketSort(array: number[], bucketSize = 5): T[] | number[] {
if (array.length < 2) {
return array;
}
// 創建桶,對桶進行排序
return this.sortBuckets(<[][]>this.createBuckets(array, bucketSize));
}
/**
* 創建桶
* @param array 待排序數組
* @param bucketSize 桶大小,即每個桶里的元素數量
*
* @return 二維數組類型的桶
*/
private createBuckets = (array: number[], bucketSize: number): number[][] => {
// 計算數組最大值與最小值
let minValue = array[0];
let maxValue = array[0];
for (let i = 1; i < array.length; i++) {
if (array[i] < minValue) {
minValue = array[i];
} else if (array[i] > maxValue) {
maxValue = array[i];
}
}
// 計算需要的桶數量,公式為: 數組最大值與最小值的差值與桶大小進行除法運算
const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1;
// 用于存放桶的二維數組
const buckets: number[][] = [];
// 計算出桶數量后,初始化每個桶
for (let i = 0; i < bucketCount; i++) {
buckets[i] = [];
}
// 遍歷數組,將每個元素分布到桶中
for (let i = 0; i < array.length; i++) {
// 計算需要將元素放到哪個桶中,公式為: 當前遍歷到的元素值與數組的最小值的差值與桶大小進行除法運算
const bucketIndex: number = Math.floor((array[i] - minValue) / bucketSize);
// 將元素放進合適的桶中
buckets[bucketIndex].push(array[i]);
}
// 將桶返回
return buckets;
};
// 對每個桶進行排序
private sortBuckets(buckets: T[][]): T[] {
const sortedArray: T[] = [];
for (let i = 0; i < buckets.length; i++) {
if (buckets[i] != null) {
// 調用插入排序
this.insertionSort(buckets[i]);
// 將排序好的桶取出來,放進sortedArray中
sortedArray.push(...buckets[i]);
}
}
return sortedArray;
}
編寫測試代碼
我們將上述圖中的例子放進代碼中看其是否能正確執行。
const array = [12, 5, 6, 7, 8, 9, 11, 3, 4, 19];
const sort = new Sort(array);
const result = sort.bucketSort(array);
console.log(result.join());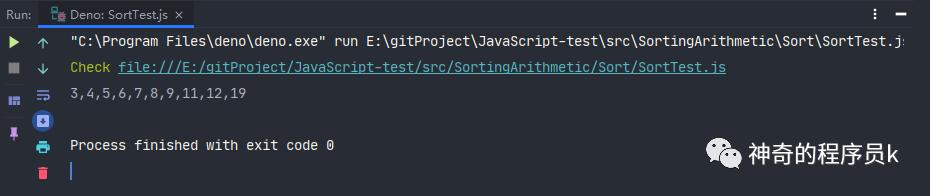
基數排序
基數排序也是一個分布式排序算法,它根據數字的有效位或基數將整數分布到桶中。比如,十進制數,使用的基數是10.因此,算法將會使用10個桶用來分布元素并且首先基于各位數字進行排序,然后基于十位數字,然后基于百位數字,以此類推。
實現思路
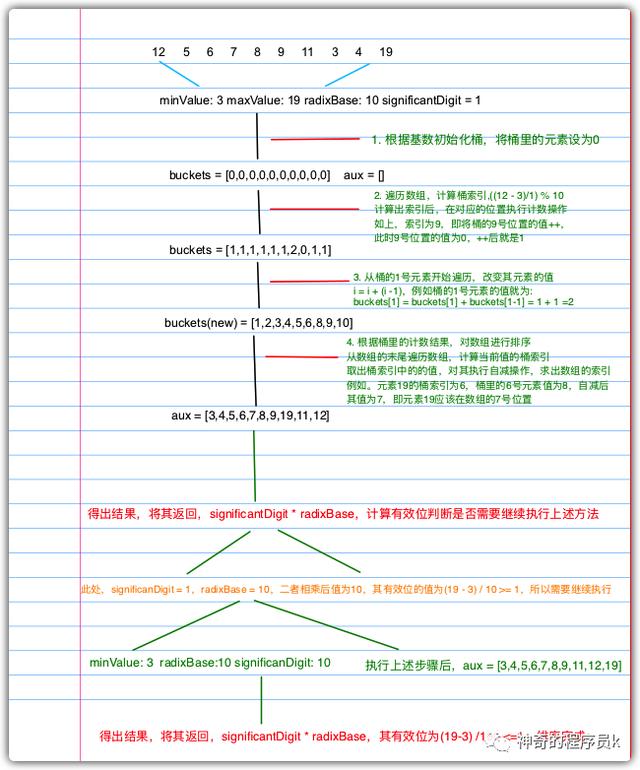
基數排序也是用來排序整數,因此我們從最后一位開始排序所有的數。首先,只會基于最后一位有效位對數字進行排序,在下次迭代時,我們會基于第二個有效位進行排序(十位數字),然后是第三個有效位(百位數字),以此類推。我們繼續這個過程直到沒有待排序的有效位,因此我們需要知道數組中的最小值和最大值。實現基數排序我們需要一個輔助函數(countingSortForRadix),即根據有效位對數組進行排序。接下來,我們先來看下基數排序主函數的實現思路。
- 創建基數排序函數(radixSort),接受2個參數:待排序數組array,基數radixBash
- 首先,獲取array的最大值maxValue和最小值minValue
- 聲明一個輔助變量significantDigit,用于存儲當前有效數字,默認從最后一位有效數字,即1
- 計算有效位,公式為:(maxValue - minValue) / significantDigit,計算出的值如果大于等于1執行下述邏輯:
- 以當前有效位作為參數調用singnificantDigit函數對數組進行排序
- 當前有效數字*基數,繼續執行上述過程
- 最后,執行完成返回排序好多的數組
接下來,我們來看下基于有效位進行排序的函數實現思路。
- 創建countingSortForRadix函數,接受4個參數:待排序數組array,基數radixBase、有效位significantDigit、數組的最小值minValue
- 聲明桶索引bucketsIndex以及桶buckets以及輔助數組aux
- 通過radixBase來初始化桶,默認初始化為0
- 遍歷array,基于有效位計算桶索引執行計數排序
- 計算桶索引,公式為:((array[i] - minValue) / significantDigt) % radixBase
- 根據桶索引,執行計數操作,即buckets[bucketsIndex++]
- 計算累積結果得到正確的計數值,從1開始遍歷到radixBase位置。
- buckets[i]等于buckets[i] 加上buckrts[i - 1]的值
- 計數完成,遍歷array將值移回原始數組中,用aux輔助數組來存儲
- 計算當前元素的桶索引bucketsIndex,公式為:((array[i] - minValue) / significantDigit) % radixBase
- 對當前桶索引內的元素執行自檢操作,得到其在數組中的正確位置index
- 計算出索引后,在aux中的對應位置存儲當前遍歷到的元素
- 最后排序完成,返回axu。
我們通過一個例子來描述上述過程,如下圖所示。
實現代碼
接下來,我們將上述思路轉換為代碼.
/**
* 基數排序
* @param array 待排序數組
* @param radixBase 10進制排序,基數為10
*/
radixSort(array: number[], radixBase = 10): number[] {
if (array.length < 2) {
return array;
}
// 獲取數組的最小值和最大值
const minValue = this.findMinValue(array);
const maxValue = this.findMaxValue(array);
// 當前有效數字,默認會從最后一位有效數字開始排序
let significantDigit = 1;
/**
* 計算有效位
* 最大值和最小值的差與有效數字進行除法運算,其值大于等于1就代表還有待排序的有效位
*/
while ((maxValue - minValue) / significantDigit >= 1) {
// 以當前有效位為參數對數組進行排序
array = this.countingSortForRadix(array, radixBase, significantDigit, minValue);
// 當前有效數字乘以基數,繼續執行while循環進行基數排序
significantDigit *= radixBase;
}
return array;
}
/**
* 基于有效位進行排序
* @param array 待排序數組
* @param radixBase 基數
* @param significantDigit 有效位
* @param minValue 待排序數組的最小值
*/
private countingSortForRadix = (array: number[], radixBase: number, significantDigit: number, minValue: number) => {
// 聲明桶索引以及桶
let bucketsIndex;
const buckets = [];
// 輔助數組,用于計數完成的值移動會原數組
const aux = [];
// 通過基數來初始化桶
for (let i = 0; i < radixBase; i++) {
buckets[i] = 0;
}
// 遍歷待排序數組,基于有效位計算桶索引執行計數排序
for (let i = 0; i < array.length; i++) {
// 計算桶索引
bucketsIndex = Math.floor(((array[i] - minValue) / significantDigit) % radixBase);
// 執行計數操作
buckets[bucketsIndex]++;
}
// 計算累積結果得到正確的計數值
for (let i = 1; i < radixBase; i++) {
buckets[i] = buckets[i] + buckets[i - 1];
}
// 計數完成,將值移回原始數組中,用aux輔助數組來存儲
for (let i = array.length - 1; i >= 0; i--) {
// 計算當前元素的桶索引
bucketsIndex = Math.floor(((array[i] - minValue) / significantDigit) % radixBase);
// 對當前桶索引內的元素執行自減操作,得到其在數組中的正確的位置
const index = --buckets[bucketsIndex];
// 計算出索引后,在aux中的對應位置存儲當前遍歷到的元素
aux[index] = array[i];
}
console.log(aux);
return aux;
};
編寫測試代碼
接下來,我們將上圖中的例子放進代碼中,觀察函數是否正確執行。
const array = [12, 5, 6, 7, 8, 9, 11, 3, 4, 19];
const sort = new Sort(array);
const result = sort.radixSort(array);
console.log(result.join());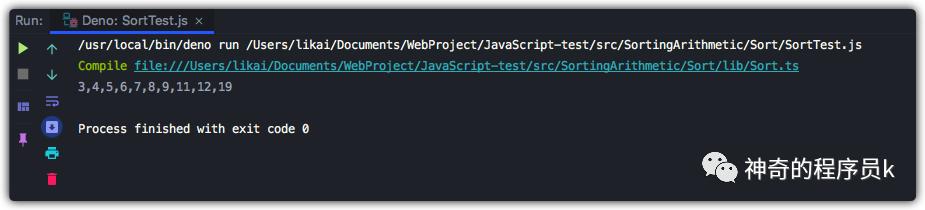
搜索算法
接下來,我們來學習搜索算法,搜索算法分為兩種:順序(線性)搜索和二分搜索。在之前文章中,我已經詳細講解了這兩種搜索算法的基礎原理以及圖解實現,所以此處只講其代碼實現。文章傳送門:數組查找: 線性查找與二分查找本文示例代碼地址:SearchArithmetic.ts
順序搜索
順序搜索是最基本的搜索算法,它會將每一個數據結構中的元素和我們要找的元素做比較。它也是最低效的一種搜索算法。
實現代碼
linearSearch(): number | null {
for (let i = 0; i < this.array.length; i++) {
if (this.array[i] === this.target) {
return i;
}
}
return null;
}
編寫測試代碼
const array = [7, 8, 1, 2, 3, 5, 12, 13, 16, 19];
const searchArithmetic = new SearchArithmetic(array, 7);
const mid = searchArithmetic.linearSearch();
console.log(mid);
二分搜索
二分搜索要求被搜索的數據結構已經排好序,它的基本原理就是找到數組的中間值,然后將目標值和找到的值進行大小比較,如果比中間值大就往中間值的右邊找,否則就往中間值的左邊找。
實現思路
- 選擇數組的中間值
- 如果選中值是待搜索值,那么算法執行完畢
- 如果待搜索值比選中值要小,則返回步驟1并在選中值左邊的子數組中尋找(較小)
- 如果待搜索值比選中值要大,則返回步驟1并在選中值右邊的子數組中尋找(較大)
實現代碼
binarySearch(): number | null {
// 對數組進行排序
this.sort.quickSort();
// 設置指針作為數組邊界
let low = 0;
let high = this.array.length - 1;
while (low <= high) {
// 獲取數組中間值
const mid = Math.floor((low + high) / 2);
// 獲取數組的中間值
const element = this.array[mid];
// 如果數組中間值小于目標值,low+1,向其右邊繼續找
if (this.compareFn(element, this.target) === Compare.LESS_THAN) {
low = mid + 1;
} else if (this.compareFn(element, this.target) === Compare.BIGGER_THAN) {
// 如果中間值大于目標值,向其左邊繼續找
high = mid - 1;
} else {
// 中間值等于目標值,元素找到,返回mid即當前元素在數組的位置
return mid;
}
}
// 未找到,返回null
return null;
}
編寫測試代碼
const array = [7, 8, 1, 2, 3, 5, 12, 13, 16, 19];
const searchArithmetic = new SearchArithmetic(array, 7);
const mid = searchArithmetic.binarySearch();
console.log(mid);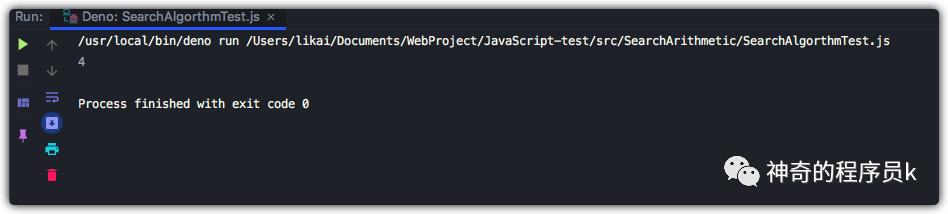
內插搜索
內插搜索是改良版的二分搜索。二分搜索總是檢查mid位置上的值,而內插搜索可能會根據要搜索的值檢查數組中的不同地方。
實現思路
它遵循以下步驟:
- 使用position公式選中一個值
- 如果待搜索值比選中值要小,則返回步驟1并在選中值左邊的子數組中尋找(較小)
- 如果待搜索值比選中值要大,則返回步驟1并在選中值右邊的子數組中尋找(較大)
實現代碼
/**
* 內插搜索
* 二分查找的優化,通過特定算法計算delta和position的值優化掉二分查找的尋找中間值做法
* @param equalsFn 校驗兩個值是否相等函數
* @param diffFn 計算兩個數的差值函數
*/
interpolationSearch(equalsFn = defaultEquals, diffFn: IDiffFunction<T> = defaultDiff): number | null {
// 排序
this.sort.quickSort();
// 獲取數組程度
const { length } = this.array;
// 定義指針,確定數組邊界
let low = 0;
let high = length - 1;
// 聲明position,用于公式
let position = -1;
let delta = -1;
// 目標值大于等于數組的low邊界值且目標值小于等于high邊界值就執行循環里的內容
while (low <= high && biggerEquals(this.target, this.array[low], this.compareFn) && lesserEquals(this.target, this.array[high], this.compareFn)) {
// 目標值與array的low邊界的值做差
// 與array的high邊界的值和low邊界的值做差
// 最后將二者得出的值做除法運算,計算出delta值
delta = diffFn(this.target, this.array[low]) / diffFn(this.array[high], this.array[low]);
// 計算比較值的位置
position = low + Math.floor((high - low) * delta);
// 如果比較值位置的元素等于目標值,則返回當前索引
if (equalsFn(this.array[position], this.target)) {
return position;
}
// 如果比較值位置的元素小于目標值,則向其右邊繼續找
if (this.compareFn(this.array[position], this.target) === Compare.LESS_THAN) {
low = position + 1;
} else {
// 如果比較值位置的元素大于目標值,則向其左邊繼續查找
high = position - 1;
}
}
// 未找到
return null;
}
編寫測試代碼
const array = [7, 8, 1, 2, 3, 5, 12, 13, 16, 19];
const searchArithmetic = new SearchArithmetic(array, 7);
const mid = searchArithmetic.interpolationSearch();
console.log(mid);
隨機算法
在日常開發中,我們會遇到將數組中的元素打亂位置,這樣的場景,那么此時我們就需要設計一種隨機算法來實現了,現實中一個很常見的場景就是洗撲克牌。
Fisher-Yates算法
此處我們講解一種隨機算法,名為Fisher-Yates,顧名思義,該算法就是由Fisher 和 Yates 創造。
實現思路
該算法的核心思想就是,從數組的最后一位開始迭代數組,將迭代到的元素和一個隨機位置進行交換。這個隨機位置比當前位置小。這樣這個就算法可以保證隨機過的位置不會再被隨機一次。下圖展示了這個算法的操作過程
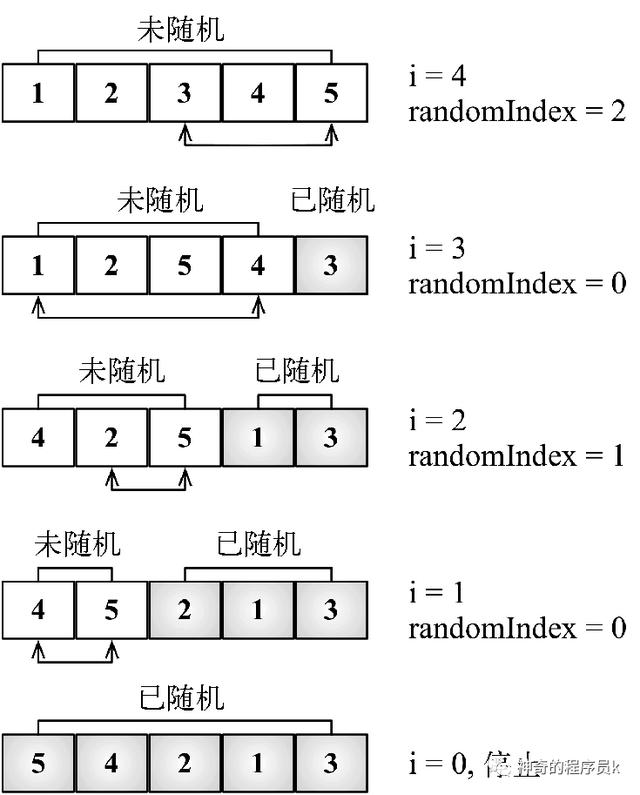
實現代碼
export class ShuffleArithmetic<T> {
constructor(private array: T[]) {}
// Fisher-Yates隨機算法
fisherYates(): T[] {
// 從數組的最后一位向前遍歷數組
for (let i = this.array.length - 1; i > 0; i--) {
// 計算隨機位置,用一個隨機數與i+1相加,得出的隨機位置一定比當前位置小
const randomIndex = Math.floor(Math.random() * (i + 1));
// 交換當前位置的元素和隨機位置的元素
this.swap(i, randomIndex);
}
return this.array;
}
/**
* 交換數組的元素
* @param a
* @param b
* @private
*/
private swap(a: number, b: number) {
const temp: T = this.array[a];
this.array[a] = this.array[b];
this.array[b] = temp;
}
}
編寫測試代碼
import { ShuffleArithmetic } from "./lib/ShuffleArithmetic.ts";
const array = [4, 5, 6, 1, 2, 3, 4, 5, 8, 9, 0, 11, 22, 41];
const shuffleArithmetic = new ShuffleArithmetic(array);
shuffleArithmetic.fisherYates();
console.log("隨機排序后的數組元素", array.join());
作者:神奇的程序員K
轉發鏈接:https://mp.weixin.qq.com/s/3B8dZRfbIuktSBeArXlmcQ






