機(jī)器學(xué)習(xí)和深度學(xué)習(xí)一直是業(yè)界的熱門話題。品牌領(lǐng)先于功能，導(dǎo)致深度學(xué)習(xí)在許多人工智能應(yīng)用中被過度使用。

這篇文章將提供對約束求解的快速理解，這是一個強(qiáng)大但未被充分利用的方法，可以解決人工智能和其他計算機(jī)科學(xué)領(lǐng)域的大量問題，例如物流和調(diào)度時間推理和圖形問題。

解決現(xiàn)實問題

讓我們來考慮一個事實性的和高度話題性的問題。

病人人數(shù)正在上升。醫(yī)院必須迅速組織起來治療病人。

世界上需要一種算法，在疾病嚴(yán)重程度、患者年齡和位置、醫(yī)院容量和設(shè)備等多個標(biāo)準(zhǔn)下，將感染者和醫(yī)院匹配起來。

許多人會說，神經(jīng)網(wǎng)絡(luò)將是最適合它的：它可以有不同的配置，廣泛的參數(shù)范圍，可以根據(jù)需要減少到一個獨(dú)特的解決方案。

然而，也有一些不利因素會破壞這個方案：

• 模型需要訓(xùn)練，因此需要以前案例的歷史數(shù)據(jù)，
• 清理和整合數(shù)據(jù)集會浪費(fèi)很多時間，
• 各種體系結(jié)構(gòu)都需要通過冗長的訓(xùn)練并且要進(jìn)行測試。

另一方面，如果用一個布爾可滿足性問題來描述，在不確定多項式時間(NP完全問題)中仍然給出次優(yōu)解，并且不需要任何歷史數(shù)據(jù)的情況下，不會有上述任何缺點(diǎn)。

這篇文章幫助你快速一覽CSPs。理論和問題的表述將被忽略。有關(guān)更嚴(yán)格的方法，請參考論文，論文在文章的末尾

抽象問題

這篇文章將介紹約束編程，旨在解決這個案例。上面那張圖說明了我們算法的輸出，應(yīng)該該算法將感染者與醫(yī)院匹配。現(xiàn)有幾個框架用于約束求解。google Optimization Tools(又稱Tools)是一個用于解決組合優(yōu)化問題的開源軟件套件。我們的問題將使用Python中的這個框架進(jìn)行建模。

from ortools.sat.python import cp_model

colab:https://colab.research.google.com/drive/1vFkt5yIQtyelqvCh2TsJ9UDeM5miXqui

參數(shù)

現(xiàn)在，讓我們將問題簡化為4個參數(shù)(1)：

• 感染者所在地
• 感染者的嚴(yán)重程度
• 醫(yī)院位置
• 每家醫(yī)院的床位數(shù)

讓我們用python定義這些參數(shù)：

# 醫(yī)院數(shù)量
n_hospitals = 3
# 感染者人數(shù)
n_patients = 200
# 每家醫(yī)院的床位數(shù)
n_beds_in_hospitals = [30,50,20]
# 病人位置，tuple (x,y)
patients_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_patients)]
# 醫(yī)院位置，tuple (x,y)
hospitals_loc = [(randint(0, 100), randint(0, 100)) for _ in range(n_hospitals)]  
# 病人嚴(yán)重等級 1~5
patients_severity = [randint(1, 5) for _ in range(n_patients)]

變量

約束滿足問題由一組變量組成，這些變量必須以滿足一組約束。

• 令I(lǐng)為醫(yī)院的集合
• 令$J_i$為醫(yī)院i的床位集合
• 令$K$為病人集合

定義變量的索引族：

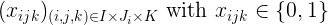
如果在醫(yī)院i中，床j由病人k取走，則$x_{ijk} = 1$。為了將醫(yī)院的每一張床與一個病人聯(lián)系起來，我們的目標(biāo)是找到一組滿足所有約束條件的變量。

我們可以將這些變量添加到模型中：

model = cp_model.CpModel()
x = {}
for i in range(n_hospitals):
  for j in range(n_beds_in_hospitals[i]):
    for k in range(n_patients):
      x[(i,j,k)] = model.NewBoolVar("x(%d,%d,%d)" % (i,j,k))

硬約束

硬約束定義了模型的目標(biāo)。它們是必不可少的，如果它們得不到解決，就無法解決問題：

• 每張床上最多只能有一個人
• 每個人最多只能有一張床

讓我們關(guān)注第一個硬約束。對于每家醫(yī)院的每一張床，我：

• 要么有一個唯一的病人k，
• 要么床是空的。

因此，可以用以下方式表示：

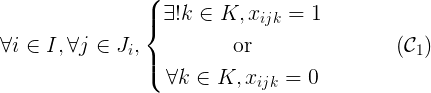
我們的求解器是一個組合優(yōu)化求解器，它只能處理整數(shù)約束。因此，必須轉(zhuǎn)化為一個整數(shù)方程：

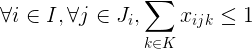
這個不等式可以加到我們的模型中。

# 每張床最多只能住一個人
for i in range(n_hospitals):
  for j in range(n_beds_in_hospitals[i]):
    model.Add(sum(x[(i,j,k)] for k in range(n_patients)) <= 1)

接下來，第二個硬約束：對于每個患者k：

• 要么他在一個唯一的病床上j在一個唯一的醫(yī)院i
• 要么他在家。

同理，可以轉(zhuǎn)化為一個整數(shù)不等式:

最后，可以將此約束添加到模型中。

# 每個人最多只能睡一張床
for k in range(n_patients):
  inner_sum = []
  for i in range(n_hospitals):
    inner_sum.Append(sum(x[(i,j,k)] for j in range(n_beds_in_hospitals[i]))) 
  model.Add(sum(inner_sum) <= 1)

軟約束

接下來是軟約束。這些都是非常需要的：我們的解決方案必須盡可能滿足它們，但它們不是找到解決方案的必要條件：

• 每個病人都應(yīng)該躺在床上
• 每個人都應(yīng)該由最近的醫(yī)院處理
• 病床不足時，應(yīng)先處理病情嚴(yán)重的病人

當(dāng)硬約束被建模為等式或不等式時，軟約束是最小化或最大化的表達(dá)式。

設(shè)Ω為滿足硬約束的所有解的集合。

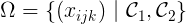
每一個病人都應(yīng)該被安排在一張床上，這意味著最大限度地增加被占用的床的數(shù)量。

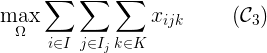
每個人都應(yīng)該由最近的醫(yī)院處理，以盡量減少每個病人與其指定醫(yī)院之間的距離。

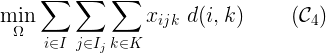
如果沒有足夠的床位，應(yīng)首先處理病情嚴(yán)重的病人，以最大限度地提高所有處理病人的總嚴(yán)重程度。通過表示sev(k)患者k的嚴(yán)重程度：

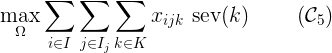
然后我們可以將所有軟約束簡化為一個目標(biāo)：

需要注意的是：這些軟約束沒有相同的定義域。

• 患者最大化約束范圍從0到n，其中n是患者數(shù)，
• 病情嚴(yán)重性限制范圍從0到5n
• 距離約束范圍從0到所有i和k的最大歐幾里得距離。

考慮到所有這些約束具有相同的優(yōu)先級，我們必須定義懲罰因子來平衡不同的約束。

下面是相應(yīng)的代碼：

# 整數(shù)的距離函數(shù)
idist = lambda xy1, xy2: int(((xy1[0]-xy2[0])**2 + (xy1[1]-xy2[1])**2)**0.5)

gain_max_patients = 140
gain_severity = int(140/5)
gain_distance = -1
#最大化的目標(biāo)
soft_csts = []
for i in range(n_hospitals):
  for j in range(n_beds_in_hospitals[i]):
    for k in range(n_patients):
      factor = 
        gain_max_patients 
        + gain_distance * idist(hospitals_loc[i], patients_loc[k]) 
        + gain_severity * patients_severity[k]
      soft_csts.append(factor * x[(i,j,k)])
model.Maximize(sum(soft_csts))

求解

現(xiàn)在我們可以啟動求解器了。它將試圖在指定的時間限制內(nèi)找到最優(yōu)解。如果無法找到最優(yōu)解，則返回最近的次優(yōu)解。

solver = cp_model.CpSolver()
solver.parameters.max_time_in_seconds = 60.0
status = solver.Solve(model)

在我們的例子中，求解器在2.5秒內(nèi)返回一個最優(yōu)解。

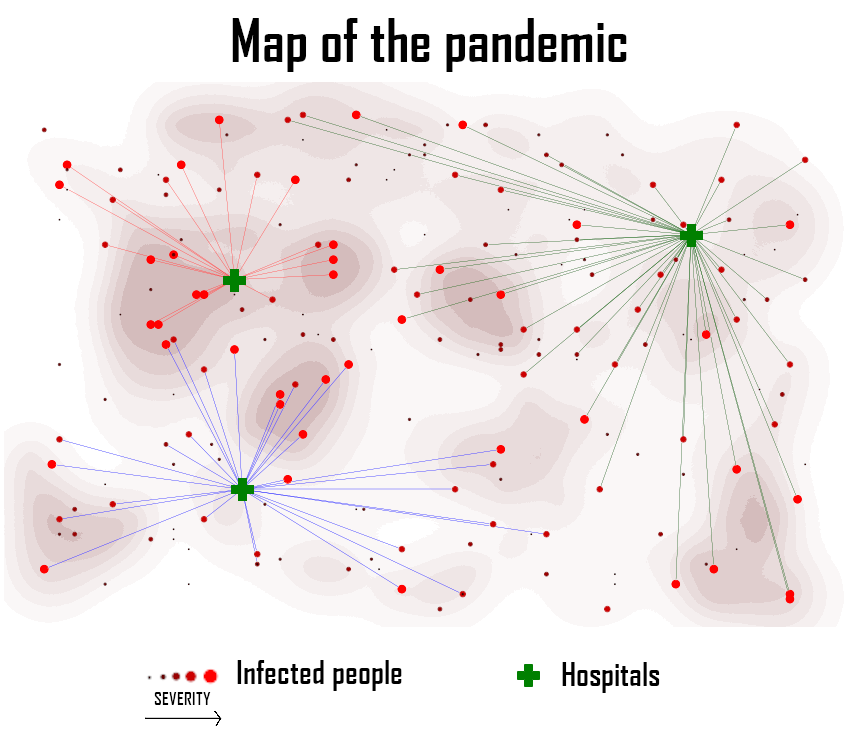
結(jié)論

要創(chuàng)建這個解決方案，只需要1小時的研究和30分鐘的編程。

如果使用深度學(xué)習(xí)，要進(jìn)行幾天的數(shù)據(jù)清理，至少一天測試不同的架構(gòu)，另一天進(jìn)行訓(xùn)練。

此外，如果模型良好，CP-SAT模型是非常健壯的。下面是不同模擬參數(shù)的結(jié)果。結(jié)果在許多不同的情況下仍然是一致的，隨著模擬參數(shù)的增加（3000名患者，1000張病床），解決方案推斷只需不到3分鐘。

當(dāng)然，csp幾乎不適用于計算機(jī)視覺和NLP等主題，在這些主題中，深度學(xué)習(xí)有時是最好的方法。然而，在物流、調(diào)度和計劃方面，這往往是可以實現(xiàn)的方法。

深度學(xué)習(xí)的炒作激發(fā)了一些人嘗試一些瘋狂的舉動來獲得認(rèn)可。有時，最好還是通過閱讀幾篇關(guān)于你正在研究的問題的調(diào)查報告再想想你應(yīng)該如何解決。

引用

[1] Jingchao Chen, Solving Rubik’s Cube Using SAT Solvers, arXiv:1105.1436, 2011.

[2] Biere, A., Heule, M., and van Maaren, H. Handbook of satisfiability, volume 185. IOS press, 2009a

[3] Knuth, D. E., The art of computer programming, Volume 4, Fascicle 6: Satisfiability. Addison-Wesley Professional, 2015

[4] Vipin Kumar, Algorithms for constraint-satisfaction problems: a survey, AI Magazine Volume 13, Issue 1, 1992.