蒙特卡洛這種方法在金融等領域得到了廣泛的應用,以便對各種風險情景進行建模。
然而,該方法在時間序列分析的其他方面也有重要的應用。在這個特定的例子中,讓我們看看蒙特卡洛方法如何被用來為web頁面瀏覽量建模。

以上時間序列來源于Wikimedia Toolforge,是從2019年1月到2020年7月維基百科上“醫療”一詞的網頁瀏覽量的時間序列。數據都是按每日劃分的。
我們可以看到,時間序列每天都顯示出顯著的波動性,并且顯示了數據中一些奇怪的“峰值”的典型特征。或者說,在這些天中,搜索該術語的次數特別高。
試圖對這樣的時間序列進行直接預測通常是徒勞的。這是因為不可能從統計學上預測搜索詞何時會出現峰值,因為這會受到獨立于過去數據的影響。例如,與健康有關的重大新聞事件會導致搜索該詞的高峰。
然而,特別有趣的是我們可以創建一個模擬,以分析web頁面統計的許多潛在場景,并估計在不正常的場景下這個搜索詞的頁面瀏覽量有多高或多低。
概率分布
當運行蒙特卡羅模擬時,重要的是要注意所使用的分布類型。
考慮到頁面瀏覽量不能為負,我們假設分布是正偏態的。
以下是數據的柱狀圖:

我們可以看到,分布顯示正偏態,有幾個離群值使分布尾部向右傾斜。
>>> series = value;
>>> skewness = series.skew();
>>> print("Skewness:");
>>> print(round(skewness,2));
Skewness:
0.17
此分布的偏態為0.17。
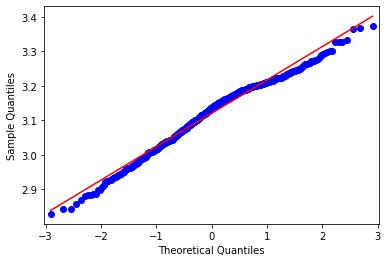
QQ圖表明,除了出現的異常值外,大多數值的分布都是正態分布。

然而,更可能的是,由于正偏態,該數據表示對數正態分布。我們將數據轉換為對數格式將導致分布的正態性。
>>> mu=np.mean(logvalue)
>>> sigma=np.std(logvalue)
>>> x = mu + sigma * np.random.lognormal(mu, sigma, 10000)
>>> num_bins = 50
這是對數數據的分布,更能代表正態分布。

此外,此分布的偏態現在為-0.41。
>>> logvalue=pd.Series(logvalue)
>>> logseries = logvalue;
>>> skewness = logseries.skew();
>>> print("Skewness:");
>>> print(round(skewness,2));
Skewness:
-0.41
這表明有輕微的負偏態,但QQ圖仍顯示正態分布。
蒙特卡羅模擬
既然數據已經被適當地轉換,就可以生成蒙特卡羅模擬來分析頁面瀏覽量統計的潛在結果范圍。頁面瀏覽量按照所選的分布以對數格式表示。
首先,計算時間序列的平均值和波動率(用標準差衡量)。
>>> mu=np.mean(logvalue)
>>> sigma=np.std(logvalue)
>>> x = mu + sigma * np.random.lognormal(mu, sigma, 10000)
>>> num_bins = 50
然后用x定義相應的數組,使用mu和sigma,再生成10000個隨機數,這些隨機數按照定義的均值和標準差遵循對數正態分布。
array([5.21777304, 5.58552424, 5.39748092, ..., 5.27737933, 5.42742056, 5.52693816])
現在,讓我們繪制直方圖。

同樣,這些值以對數格式表示。我們看到這個形狀代表正態分布。如前所述,蒙特卡羅模擬的思想不是預測網頁瀏覽量本身,而是提供在許多不同的模擬中網頁瀏覽量的估計值,以便確定
- 1)大多數網頁瀏覽量的范圍;
- 2)分布中極值的范圍。
結論
在本文中,你看到了:
- 蒙特卡羅模擬的應用
- 偏態在定義分布中的作用
- 如何進行模擬以識別獲得極值的概率






