旅行商問題 (TSP 問題) 是一個 NP-hard 問題,給定若干個城市,求旅行商從某個城市開始,遍歷所有城市最終回到出發點的最短路徑 (每個城市只經過一次)。求 TSP 的最優解時間較長,本文介紹一種用 SOM 算法求 TSP 近似解的方法,SOM 是競爭神經網絡,也稱為自組織映射。
1.前言
最近突然翻到讀大學時一個小作業的代碼,主要用 SOM 網絡算法求 TSP 問題近似解。代碼參考了論文《A simple learning algorithm for growing ring SOM and its application to TSP》,論文作者用了一種 RSOM 算法,與 SOM 不同,其初始神經元比較少,但是會在訓練的過程中不斷的增加新的神經元。
代碼是用 matlab 編寫的,地址:https://github.com/cc54294/SOM_TSP
代碼的效果如下面的 gif 所示,分別是在 48、101、225、561 個城市上計算 TSP 的結果。在 48、101、225 個城市上的效果都比較好,但是在 561 個城市上的效果比較差。

48 個城市 TSP 問題

101 個城市 TSP 問題

225 個城市 TSP 問題

561 個城市 TSP 問題
2.TSP 問題
TSP 問題稱為旅行商問題,問題的定義:有一個旅行商需要訪問 N 個城市,旅行商從一個城市出發,需要經過所有的 N 個城市且每個城市只經過一次,最后回到出發點,求最短的路徑。如下圖所示,從城市 A 出發,左側為 TSP 問題的最短路徑:

TSP 問題
之前介紹過 Pointer Network,可用于求解 TSP 問題,不熟悉的童鞋可以參考一下之前的文章《指針網絡 Pointer Network》。本文介紹另一種神經網絡 SOM 用于求解 TSP。
3.SOM 算法
SOM 神經網絡 (自組織映射 Self-Organizing Map),是一種競爭型神經網絡,通常用于無監督學習。一般的神經網絡通過損失函數計算梯度進行優化,而 SOM 采用了競爭的策略。
對于每一個輸入樣本 x,SOM 會計算所有神經元與 x 的距離 (例如歐式距離),選出獲勝神經元 (也稱為激活神經元,距離最近的),然后優化獲勝神經元附近的網絡拓撲結構。常見 SOM 結構如下,包括輸入層和輸出層 (競爭層):

SOM 示意圖
上面的圖中,輸入層的維度是 d (即每一個樣本 x 維度是 d),上面的二維網格中每一個圓點均是一個神經元,每個神經元都具有一個特征向量 w (維度也是 d)。
神經元之間是具有拓撲結構的,常見的拓撲結構有矩形 (Rectangular) 和六邊形 (Hexagonal) 的,如下:

SOM 神經元常見的拓撲結構
SOM 訓練的過程如下:
- 隨機初始化輸出層神經元的特征向量 w,維度是 d。
- 對于每一個輸入樣本 x,找出與其最匹配的神經元,可以根據歐氏距離匹配,計算所有神經元和樣本 x 的歐式距離,選距離最近的神經元作為獲勝神經元 I。

選擇與 x 距離最近的神經元 I
- 找到獲勝神經元 I 后,需要更新神經元 I 和其鄰居節點 (即拓撲結構上的鄰居) 的特征向量 w 值,更新的時候有更新權重,越靠近 I 的神經元更新權重越大。對于神經元 j,其更新權重可以用下面的公式計算:

神經元 j 的更新權重
- 得到更新權重后,可以更新神經元的特征向量 w。更新的公式如下,主要是把特征向量往 x 的方向移動。

更新神經元的特征向量
訓練完成后,輸出層的神經元可以按照聯系的緊密程度劃分為幾個部分,每部分代表一個簇或者一個類,如下圖所示:

訓練完成后,神經元可以劃分為不同的簇
4.用 RSOM 求解 TSP
RSOM (Ring SOM) 是一種特殊的 SOM 網絡,和上面說的 SOM 主要有兩個區別:
- RSOM 輸出層的神經元拓撲結構是環形的。
- 輸出層神經元個數不是固定的,會隨著訓練不斷增加神經元。
RSOM 的結構如下所示:
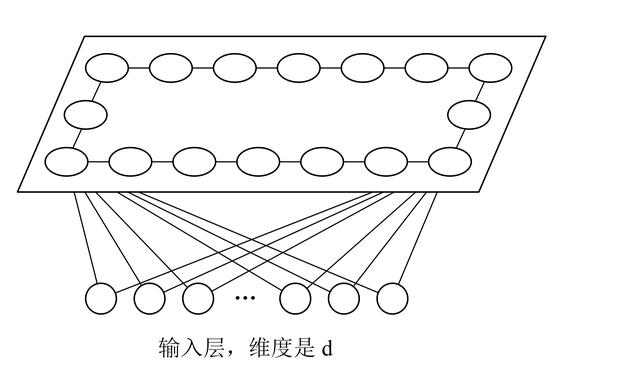
RSOM 示意圖
RSOM 訓練時的超參數包括:Tint (每更新 Tint 次,就在輸出層插入一個新的神經元),Tmax (最大的訓練次數),N(t) (t 時刻神經元的總個數),Ci(t) (t 時刻神經元 i 獲勝的次數)。RSOM 訓練過程如下:
- 隨機初始化 N(0) 個神經元,所有神經元的計數 Ci(0) = 0。
- 對于一個輸入 x,使用歐氏距離找出獲勝神經元 I。
- 更新神經元 I 及其鄰居節點的特征向量。
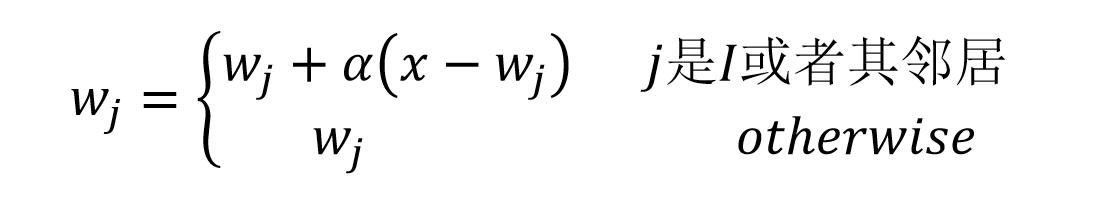
更新獲勝神經元及其鄰居的特征向量
- 獲勝神經元的計數器 CI(t) 加 1,其鄰居不用加。
- 如果更新了 Tint 次,則需要增加一個新的節點,新的節點在獲勝神經元和其鄰居之間添加。獲勝神經元 I 有左右兩個鄰居 (因為環形的),選擇距離遠的鄰居 f,并在 I 和 f 中間添加新神經元 r。新神經元 r 的特征向量是 I 和 f 特征向量的均值,同時修改新神經元 r 和獲勝神經元 I 的計數器:
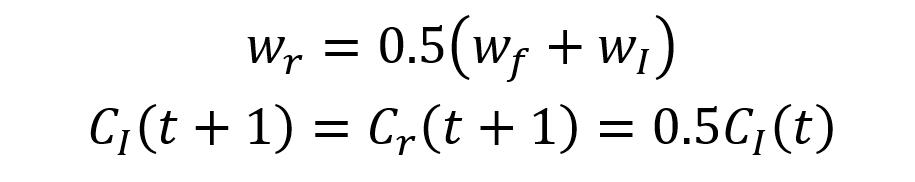
新神經元 r 的特征向量和計數器值
通過上面的步驟即可訓練 RSOM 網絡,在求解 TSP 問題時,輸入樣本 x 就是城市的坐標 (一般是 2 維,包含 x,y),每個神經元的特征向量維度也是 2。訓練時每個城市都會找出一個獲勝神經元,然后把該神經元及其鄰居都拉向城市的坐標。可以理解為有個橡皮筋,每個城市把橡皮筋往自己的方向拉,最終橡皮筋上的不同點會固定到不同的城市中,如下圖所示。

RSOM 求解 TSP 示意圖
上圖中的黑色點代表城市,白色點代表神經元,紅色點代表獲勝神經元。
5.參考文獻
A simple learning algorithm for growing ring SOM and its Application to TSP






