作者：愛做夢的魚

原文：https://blog.csdn.net/weixin_43124279/article/details/107314686

示例 1:

輸入: nums1 = [1,2,2,1], nums2 = [2,2]

輸出: [2,2]

示例 2:

輸入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]

輸出: [4,9]

說明：

輸出結果中每個元素出現(xiàn)的次數(shù)，應與元素在兩個數(shù)組中出現(xiàn)的次數(shù)一致。

我們可以不考慮輸出結果的順序。

進階:

如果給定的數(shù)組已經排好序呢？你將如何優(yōu)化你的算法？

如果 nums1 的大小比 nums2 小很多，哪種方法更優(yōu)？

如果 nums2的元素存儲在磁盤上，磁盤內存是有限的，并且你不能一次加載所有的元素到內存中，你該怎么辦？

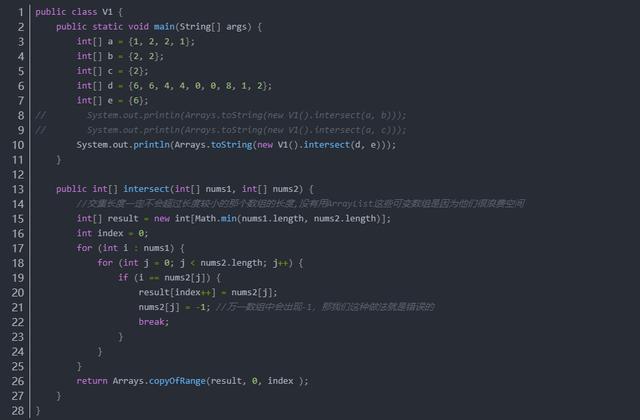
方法一：簡單、暴力（有問題）

方法二：哈希表

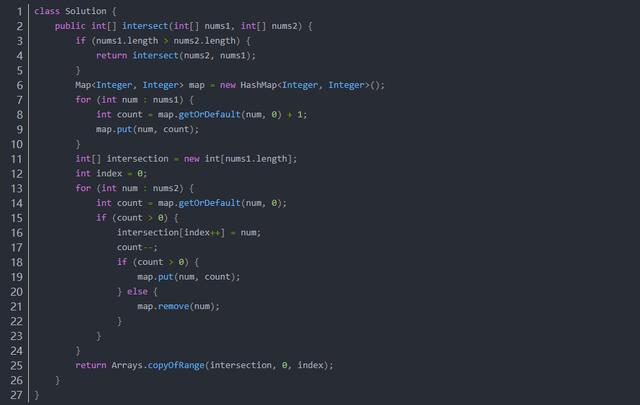
由于同一個數(shù)字在兩個數(shù)組中都可能出現(xiàn)多次，因此需要用哈希表存儲每個數(shù)字出現(xiàn)的次數(shù)。對于一個數(shù)字，其在交集中出現(xiàn)的次數(shù)等于該數(shù)字在兩個數(shù)組中出現(xiàn)次數(shù)的最小值。

首先遍歷第一個數(shù)組，并在哈希表中記錄第一個數(shù)組中的每個數(shù)字以及對應出現(xiàn)的次數(shù)，然后遍歷第二個數(shù)組，對于第二個數(shù)組中的每個數(shù)字，如果在哈希表中存在這個數(shù)字，則將該數(shù)字添加到答案，并減少哈希表中該數(shù)字出現(xiàn)的次數(shù)。

為了降低空間復雜度，首先遍歷較短的數(shù)組并在哈希表中記錄每個數(shù)字以及對應出現(xiàn)的次數(shù)，然后遍歷較長的數(shù)組得到交集。

復雜度分析

時間復雜度：O(m+n)，其中 mm 和 nn 分別是兩個數(shù)組的長度。需要遍歷兩個數(shù)組并對哈希表進行操作，哈希表操作的時間復雜度是 O(1)，因此總時間復雜度與兩個數(shù)組的長度和呈線性關系。

空間復雜度：O(min(m,n))，其中 mm 和 nn 分別是兩個數(shù)組的長度。對較短的數(shù)組進行哈希表的操作，哈希表的大小不會超過較短的數(shù)組的長度。為返回值創(chuàng)建一個數(shù)組 intersection，其長度為較短的數(shù)組的長度。

方法三：排序

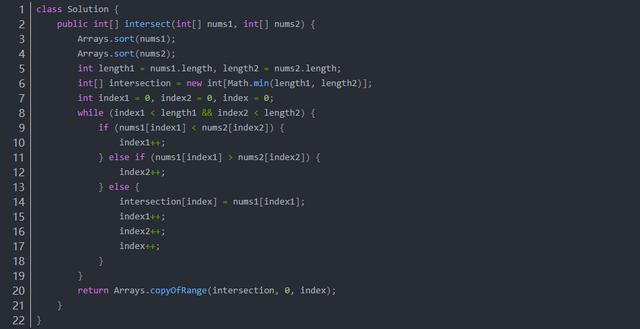
如果兩個數(shù)組是有序的，則可以便捷地計算兩個數(shù)組的交集。

首先對兩個數(shù)組進行排序，然后使用兩個指針遍歷兩個數(shù)組。

初始時，兩個指針分別指向兩個數(shù)組的頭部。每次比較兩個指針指向的兩個數(shù)組中的數(shù)字，如果兩個數(shù)字不相等，則將指向較小數(shù)字的指針右移一位，如果兩個數(shù)字相等，將該數(shù)字添加到答案，并將兩個指針都右移一位。當至少有一個指針超出數(shù)組范圍時，遍歷結束。

復雜度分析

時間復雜度：O(mlogm+nlogn)，其中 mm 和 nn 分別是兩個數(shù)組的長度。對兩個數(shù)組進行排序的時間復雜度是 O(mlogm+nlogn)，遍歷兩個數(shù)組的時間復雜度是 O(m+n)，因此總時間復雜度是O(mlogm+nlogn)。

空間復雜度：O(min(m,n))，其中 mm 和 nn 分別是兩個數(shù)組的長度。為返回值創(chuàng)建一個數(shù)組 intersection，其長度為較短的數(shù)組的長度。不過在 C++ 中，我們可以直接創(chuàng)建一個 vector，不需要把答案臨時存放在一個額外的數(shù)組中，所以這種實現(xiàn)的空間復雜度為 O(1)。

結語

如果 nums2的元素存儲在磁盤上，磁盤內存是有限的，并且你不能一次加載所有的元素到內存中。那么就無法高效地對nums2進行排序，因此推薦使用方法二而不是方法三。在方法二中，nums2 只關系到查詢操作，因此每次讀取nums2中的一部分數(shù)據(jù)，并進行處理即可。