本文是對 Monte Carlo Tree Search – beginners guide 這篇文章的文章大體翻譯,以及對其代碼的解釋。
1 引言
蒙特卡洛樹搜索在2006年被Rémi Coulom第一次提出,應用于Crazy Stone的圍棋游戲。
- Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search
蒙特卡洛樹搜索大概的思想就是給定一個游戲狀態,去選擇一個最佳的策略/動作。
1.1 有限雙人零和序貫博弈
蒙特卡洛樹搜索實際上是一個應用非常廣泛的博弈框架,這里我們將其應用于 有限雙人序貫零和博弈 問題中。像圍棋、象棋、Tic-Tac-Toe都是有限雙人序貫零和博弈游戲。
1.2 怎樣去表示一個游戲?
我們采用 博弈樹 (Game Tree)來表示一個游戲:每個結點都代表一個 狀態 (state),從一個 結點 (node)移動一步,將會到達它的 子節點 (children node)。子節點的個數叫作 分支因子 (branching factor)。 根節點 (Root node)表示初始狀態(initial state)。 終止節點 (terminal nodes)沒有子節點了。
在 tic-tac-toe 游戲中表示如下圖所示:

- 每次都是從 初始狀態 、樹的 根結點 開始。在 tic-tac-toe 游戲里面初始狀態就是一張空的棋盤。
- 從一個節點轉移到另一個節點叫作一個 move 。
- 分支因子 (branching factor), tic-tac-toe 中樹越深,分支因子也越少,也就是 children node 的數量越少。
- 游戲結束表示 終止節點 。
- 從根節點到終止節點一次表示一個單個游戲 playout 。
你不需要關系你是怎么來到這個 node ,只需要做好之后的事情就好了。
1.3 最佳策略是什么?minimax和alpha-beta剪枝
我們希望找到的就是 最佳策略 ( the most promising next move )。如果你知道對手的策略那你可以爭對這個策略求解,但是大多數情況下是不知道對手的策略的,所以我們需要用 minimax 的方法,假設你的對手是非常機智的,每次他都會采取最佳策略。
假設A與B博弈,A期望最大化自己的收益,因為是零和博弈,所以B期望A的收益最小,Minimax算法可描述為如下形式:
- 和 是玩家 和 的效益函數。
- move 表示從當前狀態 和采取的動作 轉移到下一個狀態。
- eval 評估最終的游戲分數。
- 是最終的游戲狀態。
簡單地說,就是給定一個狀態 期望找到一個動作 在對手最小化你的獎勵的同時找到一個最大化自己的獎勵。
Minimax 算法最大的弱點 就是需要擴展整棵樹,對于高分支因子的游戲,像圍棋、象棋這種,算法就很難處理。
對于上述問題的一種解決方法就是擴展樹結構到一定的閾值深度( expand our game tree only up to certain threshold depth d )。因此我們需要一個評估函數,評估 非終止節點 。這對于我們人類來說依據當前棋勢判斷誰輸誰贏是很容易做到的。計算機的解決方法可以參考原文中的:
- Chess position evaluation with convolutional neural network in Julia
另一種解決樹擴展太大的方法就是 alpha-beta剪枝算法 。它會避免一些分支的展開,它最好的結果就是與minimax算法效果相同,因為它減少了搜索空間。
2 蒙特卡洛樹搜索(MCTS)基本概念
蒙特卡洛通過多次模擬仿真,預測出最佳策略。最核心的東西就是搜索。搜索是對整棵博弈樹的組合遍歷,單次的遍歷是從根結點開始,到一個未完全展開的節點(a node that is not full expanded)。未完全展開的意思就是它至少有一個孩子節點未被訪問,或者稱作未被探索過。當遇到未被完全展開過的節點,選擇它的一個未被訪問的childre node做根結點,進行一次模擬(a single playout/simulation)。仿真的結果反向傳播(propagated back)用于更新當前樹的根結點,并更新博弈樹節點的統計信息。當整棵博弈樹搜索結束后,就相當于拿到了這顆博弈樹的策略。
我們再理解一下以下幾個關鍵概念:
- 怎么解釋 展開 或 未完全展開 (not fully unexpanded)的博弈樹節點?
- 搜索過程中的 遍歷 (traverse down)是什么?子節點如何選擇?
- 什么是 模擬仿真 (simulation)?
- 什么是 反向傳播 (backpropagation)?
- 擴展的樹節點中反向傳播、更新哪些統計( statistics )信息?
- 怎么依據策略(博弈樹)選擇動作?
2.1 模擬/Simulation/Playout
Playout/simulation是與游戲交互的一個過程,從當前節點移動到終止節點。在simulation過程中move的選擇基于rollout policy function:
Rollout Policy也被稱作快速走子策略,基于一個狀態 選擇一個動作 。為了讓這個策略能夠simulation快,一般選用隨機分布(uniform random)。如下圖所示

2.1.1 Alpha Zero中的Playout/Simulation
在AlphaGo Zero里面DeepMind‘s直接用一個CNN殘差網絡輸出position evaluation和moves probability。
2.2 博弈樹節點的擴展-全擴展、訪問節點
一個節點如果被訪問過了,意味著某個某個simulation是以它為起點的。如果一個節點的所有子節點都被訪問過了,那這個節點就稱為是完全擴展的,否則就是未完全擴展的。如下圖對比所示:

在實際過程中,一開始根節點的所有子節點都未被訪問,從中選一個,第一次simulation就開始了。
Simulation過程中rollout policy選擇子節點是不被考慮為這個子節點被訪問過了, 只有Simulation開始的節點被標記為訪問過的 。
2.3 反向傳播Simulation結果
從一個近期訪問過的節點(有時候也叫做葉結點(left node))做Simulation,當他Simulation完成之后,得出來的結果就需要反向傳播回當前博弈樹的根結點,Simulation開始的那個節點被標記為訪問過了。

反向傳播是從葉結點(simulation 開始的那個節點)到根結點。在這條路徑上所有的節點統計信息都會被計算更新。
2.4 Nodes’ statistics
拿到simulation的結果主要更新兩個量:所有的simulation reward 和所有節點 (包括simulation開始的那個節點)的訪問次數 。
- - 表示一個節點 的 simulation reward和 ,最簡單形式的就是所有考慮的節點的模擬結果之和。
- - 表示節點的另一個屬性,表示這個節點在反向傳播路徑中的次數(也表示它有多少次參與了total simulation reward)的計算。
2.5 遍歷博弈樹
搜索開始時,沒有被訪問過的節點將會首先被選中,然后simulation,結果反向傳播給根結點,之后根節點就可以被認為是全展開的。
為了選出我們路徑上的下一個節點來開始下一次模擬,我們需要考慮 的所有子節點 , , , 和其本身節點 的信息,如下圖所示:

當前的狀態被標記為藍色,上圖它是全展開的,因此它被訪問過了并且存儲了節點的統計信息:總的仿真回報和訪問次數,它的子節點也具備這些信息。這些值組成了我們最后一個部分:樹的置信度上界(Upper Confidence Bound Applied to Trees,UCT)。
2.6 置信度上界
UCT是蒙特卡羅樹搜索中的一個核心函數,用來選擇下一個節點進行遍歷:
蒙特卡洛樹搜索的過程中選UCT最大的那個遍歷。
UCT 中第一部分是 ,也被稱作 exploitation component ,可以看作是子節點 的勝率估計(總收益/總次數=平均每次的收益)。
看起來這一項已經有足夠說服力,因為只要選擇勝率高的下一步即可,但是為什么不能只用這一個成分呢?這是因為這種貪婪方式的搜索會很快導致游戲結束,這往往會導致搜索不充分,錯過最優解。因此UCT中的第二項稱為exploration component。這個成分更傾向于那些未被探索的節點( 較小)。在蒙特卡洛樹搜索過程中第二項的取值趨勢大概如下圖所示,隨著迭代次數的增加其值也下降:

參數
用于平衡MCTS中的exploitation和exploration。
2.6.1 UCT in Alpha Go and Alpha Zero
在AlphaGo Lee和Alpha Zero算法里面,UCT公式如下:
是來自策略網絡的move先驗概率,策略網絡是從狀態得到move分布的函數,目的是為了提升探索的效率。
當游戲視角發生變化的時候exploitation component 也會發生變化。
2.6.2 Alpha Go和Alpha Zero中的策略網絡
在 AlphaGo 算法里,有兩個policy網絡:
- SL Policy Network :基于人類數據的監督學習所得的網絡。
- RL Policy Network :基于強化學習自我博弈改進SL Policy Network。
Interestingly – in Deepmind’s Monte Carlo Tree Search variant – SL Policy Network output is chosen for prior move probability estimation as it performs better in practice (authors suggest that human-based data is richer in exploratory moves). What is the purpose of the RL Policy Network then? The stronger RL Policy Network is used to generate 30 mln positions dataset for Value Network training (the one used for game state evaluation)
在Alpha Zero里面只有一個網絡 ,它不僅是值網絡還是策略網絡。 It is trained entirely via self-play starting from random initialization. There is a number of networks trained in parallel and the best one is chosen for training data generation every checkpoint after evaluation against best current neural network.
2.7 終止MCTS
我們應該什么時候結束MCTS過程?如果你開始玩,那么你的“思考時間”可能是有限的(“thinking time” is probably limited),計算能力也是有限的(computational capacity has its boundaries, too)。因此最保險的做法是在你資源允許的情況下盡可能全展開遍歷搜索。
當MSCT程序結束時,最佳的移動通常是訪問次數最多的那個節點。因為在多次訪問的情況下,評估它的 值必須很高。
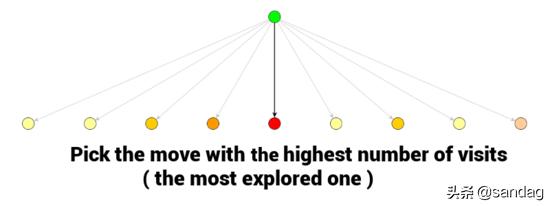
當你使用蒙特卡洛樹搜索選擇了一個動作,在對手眼里,你的這個選擇將會變成狀態的一部分。反過來對你也是一樣的,當對手選擇了一個狀態之后,你的蒙特卡洛樹搜索就可以開始工作了。利用之前的統計信息直接搜索就可以得出結果了。
3 MCTS總結
def monte_carlo_tree_search(root):
while resources_left(time, computational power):
leaf = traverse(root) # leaf = unvisited node
simulation_result = rollout(leaf)
backpropagate(leaf, simulation_result)
return best_child(root)
def traverse(node):
while fully_expanded(node):
node = best_uct(node)
return pick_univisted(node.children) or node # in case no children are present / node is terminal
def rollout(node):
while non_terminal(node):
node = rollout_policy(node)
return result(node)
def rollout_policy(node):
return pick_random(node.children)
def backpropagate(node, result):
if is_root(node) return
node.stats = update_stats(node, result)
backpropagate(node.parent)
def best_child(node):
pick child with highest number of visits






