作者:Runsen
二項(xiàng)分布
包含n個相同的試驗(yàn) 每次試驗(yàn)只有兩個可能的結(jié)果:“成功”或“失敗”。出現(xiàn)成功的概率p對每一次試驗(yàn)是相同的,失敗的概率q也是如此,且p+q=1。試驗(yàn)是互相獨(dú)立的。試驗(yàn)成功或失敗可以計數(shù),即試驗(yàn)結(jié)果對應(yīng)于一個離散型隨機(jī)變量。
以X表示n次重復(fù)獨(dú)立試驗(yàn)中事件A(成功)出現(xiàn)的次數(shù),則

在Python中,可以使用scipy.stats模塊中的binom.rvs()方法生成符合二項(xiàng)分布的離散隨機(jī)變量。該方法的參數(shù)n表示n次重復(fù)獨(dú)立試驗(yàn),p表示事件A出現(xiàn)的次數(shù)。size表示做多少次二項(xiàng)分布試驗(yàn)。
同時,本文中使用seaborn的distplot方法繪制隨機(jī)變量分布的直方圖。在大數(shù)據(jù)量的試驗(yàn)下,通過隨機(jī)變量出現(xiàn)的頻率除以試驗(yàn)的次數(shù),可以得到特定離散隨機(jī)變量出現(xiàn)的概率。
from scipy.stats import binom
import seaborn as sns
data_binom = binom.rvs(n=10,p=0.5,size=10000)
ax = sns.distplot(data_binom,
kde=False,
color='green',
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Binomial Distribution', ylabel='Frequency')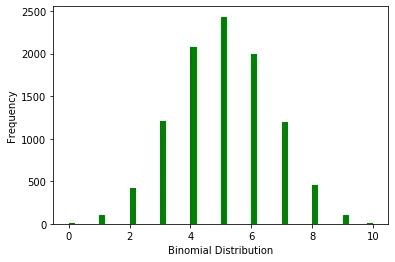
# 可以打印隨機(jī)變量的值,按照定義,其值為出現(xiàn)A事件的次數(shù),范圍肯定在[0,1]
print(data_binom)
[2 3 6 ... 5 4 3]
以拋硬幣試驗(yàn)解析上圖,得出連續(xù)拋10次硬幣,5次為正面的概率最高,概率趨近于2500/10000=25%。
貝努里分布(Bernoulli Distribution)
貝努里分布為特殊的二項(xiàng)分布,即每次執(zhí)行一次試驗(yàn)(n=1),然后獲取單次試驗(yàn)的隨機(jī)變量的值,為0或1。所以貝努里分布也被稱為0-1分布。其分布函數(shù)為:

在python中,可以使用scipy.stats模塊中的bernoulli.rvs()方法生成符合二項(xiàng)分布的離散隨機(jī)變量。其它參數(shù)同二項(xiàng)分布。
from scipy.stats import bernoulli
data_bern = bernoulli.rvs(size=10000,p=0.5)
ax= sns.distplot(data_bern,
kde=False,
color="green",
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Bernoulli Distribution', ylabel='Frequency')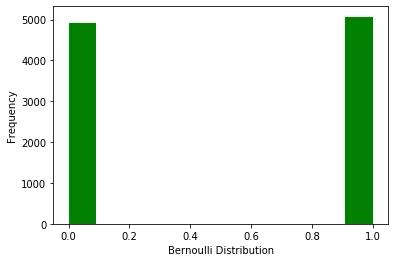
以拋硬幣試驗(yàn)解析上圖,得出正面和反面出現(xiàn)的概率,趨近于5000/10000=50%。
幾何分布(Geometric distribution)
幾何分布是指在n次貝努里試驗(yàn)中,經(jīng)過k次獲得1次成功的概率。
幾何分布的特點(diǎn):
(1)進(jìn)行一系列相互獨(dú)立的試驗(yàn);
(2)每一次試驗(yàn)既有成功的可能,也有失敗的可能,且單次試驗(yàn)的成功概率相同;
(3)主要是為了取得第一次成功需要進(jìn)行多少次試驗(yàn)。
其分布函數(shù)為:

在python中,可以使用scipy.stats模塊中的geom.rvs()方法得出幾何分布的離散隨機(jī)變量。
from scipy.stats import geom
data_geom = geom.rvs(size=10000,p=0.5)
ax= sns.distplot(data_geom,
kde=False,
color="green",
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Geometric Distribution', ylabel='Frequency')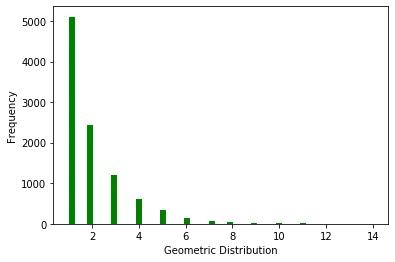
泊松分布(Poisson distribution)
泊松分布是用來描述在一指定時間范圍內(nèi)或在指定的面積或體積之內(nèi)某一事件出現(xiàn)的次數(shù)的分布,例如某企業(yè)每月發(fā)生事故的次數(shù)。
泊松分布的公式為:
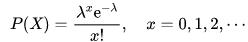
式中,為給定的時間間隔內(nèi)事件的平均數(shù)。
在python中,可以使用scipy.stats模塊中的poisson.rvs()方法得出泊松分布的連續(xù)隨機(jī)變量。其中參數(shù)mu即為公式中的,其它參數(shù)同上文方法。
from scipy.stats import poisson
data_poisson = poisson.rvs(mu=3, size=10000)
ax = sns.distplot(data_poisson,
bins=30,
kde=False,
color="green",
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Poisson Distribution', ylabel='Frequency')
正態(tài)分布(Normal Distribution)
在連續(xù)型隨機(jī)變量中,最重要的一種隨機(jī)變量是具有鐘形概率分布的隨機(jī)變量。人們稱它為正態(tài)隨機(jī)變量,相應(yīng)的概率分布稱為正態(tài)分布。
如果隨機(jī)變量X的概率密度為:

則稱X服從正態(tài)分布,記作,其中,,, 為隨機(jī)變量X的均值,為隨機(jī)變量X的標(biāo)準(zhǔn)差,它們是正態(tài)分布的兩個參數(shù)。
在python中,可以使用scipy.stats模塊中的norm.rvs()方法產(chǎn)生符合二項(xiàng)分布的連續(xù)隨機(jī)變量。其中參數(shù)loc代表隨機(jī)變量的均值,size變量代表隨機(jī)變量的標(biāo)準(zhǔn)差。
from scipy.stats import norm
# 生成標(biāo)準(zhǔn)正態(tài)分布,N(0,1)
data_normal = norm.rvs(size=10000,loc=0,scale=1)
ax = sns.distplot(data_normal,
bins=100,
kde=True,
color="green",
hist_kws={"linewidth": 15,'alpha':1})
ax.set(xlabel='Normal Distribution', ylabel='Frequency')
總結(jié)
本文通過scipy.stats包中的隨機(jī)分布函數(shù)rvs方法(Random variates),執(zhí)行10000次隨機(jī)變量的計算,通過隨機(jī)變量值個數(shù)直方圖的繪制得出特定分布的圖形。另外,也可以通過隨機(jī)分布函數(shù)的pmf方法直接獲得指定參數(shù)下的概率值,然后畫出參數(shù)與概率的對應(yīng)關(guān)系,但在本文中不做展開。






