只要你學過數據結構與算法分析，相信你對KMP算法應該都不陌生吧？如果你沒聽過，不要緊，今天我們就來聊一聊這個算法。建議最好拿一張草稿紙，然后邊看邊理解，這樣更有助于你對它的理解，更能理解它背后的精髓所在，相信你在理解完該算法之后，一定會大喊一聲：妙啊！

KMP算法的誕生

KMP算法是三位大牛：Knuth、Morris和Pratt同時發現的，于是取了他們名字的首字母然后組合起來，就成了該算法的命名。

KMP算法要解決的問題就是查找一個字符串str2是否在另一個字符串str1出現過，也即str1是否包含str2這個子串，舉個例子，可以看到下圖，str1中包含有str2這個子串(aab)。

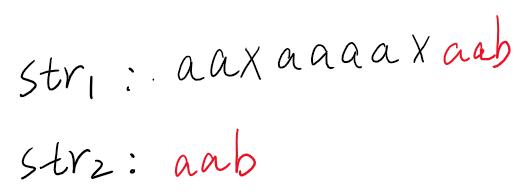
暴力解

如果想要解決這個問題，我們很容易想到的一個算法是直接暴力遍歷解，從左到右一個個匹配。

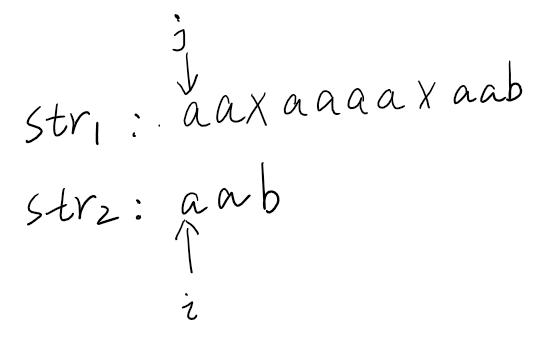
如果這個過程中有某個字符不匹配，之后我們只需要比較i指針指向的字符和j指針指向的字符是否一致。如果一致就都向后移動，如果不一致，如圖，i和j指針指向的字符不相等。

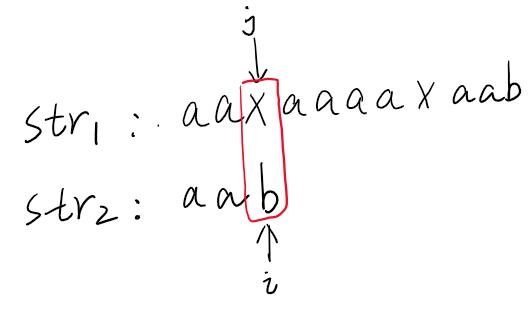
str2右移動一位，然后繼續以上操作.

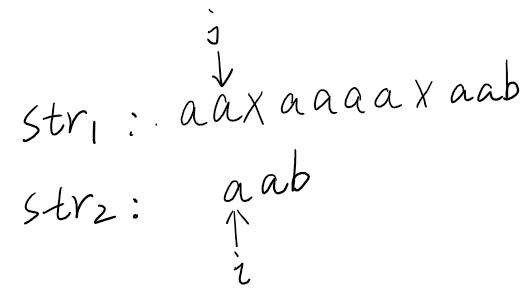
直到遍歷結束，最后匹配成功，可以返回str1包含str2.

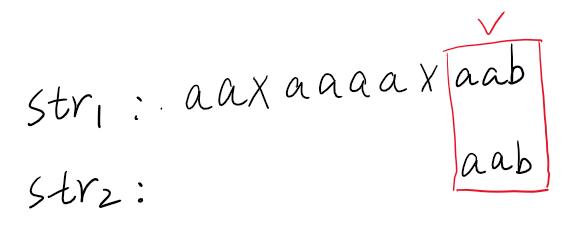
這種暴力的算法簡單粗暴，可以解決該問題，其時間復雜度為O(M*N)，M為str1的長度，N為str2的長度。KMP是對暴力解的一個優化，時間復雜度能做到O(M+N)，它的核心精髓是利用了以前的比較信息，然后推斷此次比較。說起來有點抽象，繼續舉個例子。

KMP算法

str1和str2剛開始按照從左到右遍歷的順序依次比較，發現到下標為10的時候，b不等于x，那么此時該怎么做？

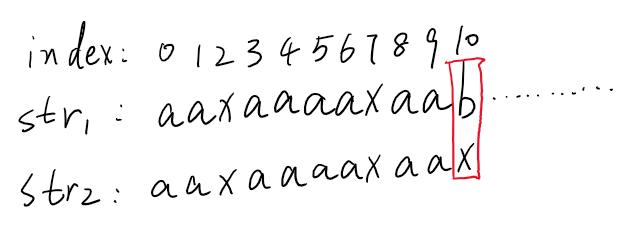
如果按照暴力的方法，是要將str2整個串往右移動一位，然后再次從左到右依次比較。

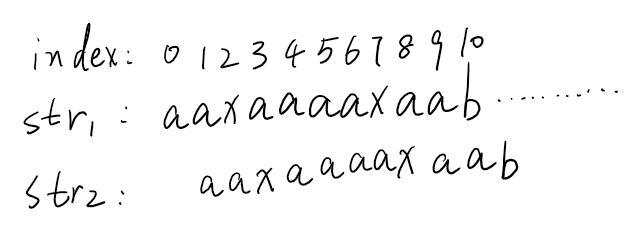
我們想一下，我們有沒有必要將str2向右移動一位，然后再從左到右依次比較呢？如果有必要的話，那它的前提條件必定是下圖中紅色圈起來的兩個范圍全部匹配上！但是如果我們事先已經知道如果str2右移一位，然后紅色圈起來的范圍是不可能匹配成功的，我們就不需要讓str2右移一位，而讓str2右移若干位。這就是KMP的精髓！

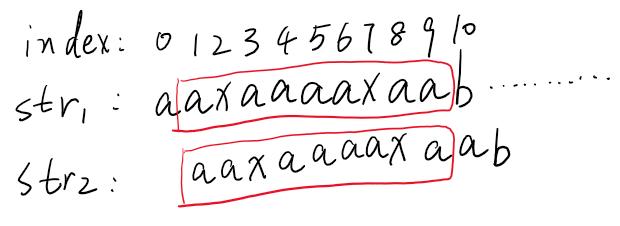
那么我們到底怎么樣才能知道str2到底向右移動幾位呢？又是怎么知道str2右移一位是不可能匹配成功的呢？我們還是首先回到第一輪的匹配中。我們已經說了，str2能夠右移一位的前提是要下圖中綠色兩塊的字符要全部匹配上，我們才右移動一位，不能再傻傻地無腦向右移動一位了。

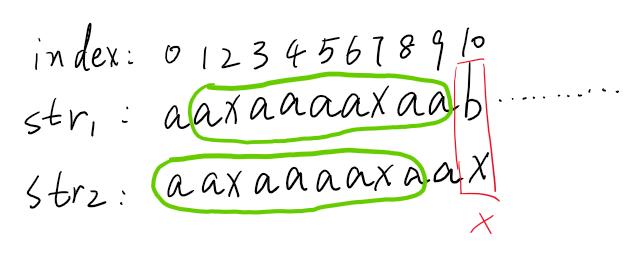
那么在第一次的比較中，我們發現下標0~9范圍內，str1和str2是全部匹配的，換句話說，str2中的綠色兩塊要完全匹配，我們才右移動！那我們怎么知道str2中的兩塊綠色是否完全匹配呢？這就又引出了一個KMP中的核心內容——前綴與后綴的最大匹配長度（也就是next數組）。

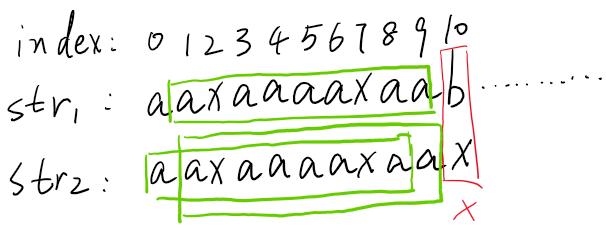
前綴與后綴的最大匹配長度

舉個簡單的例子，一個字符串abcabck，那么對于k字符來講，它前面的字符串所構成的前綴與后綴最大匹配長度為3，如下圖所示。

那么這玩意有什么用呢？回到剛才的例子

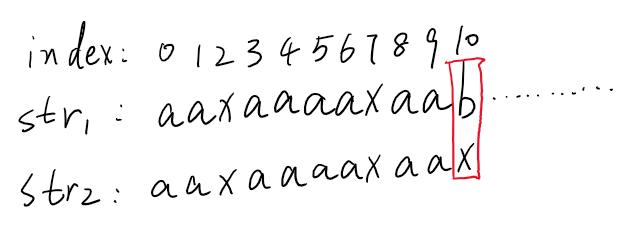
我們看一下str2相對于下標為10的字符前面的字符串所構成的前綴與后綴最大匹配長度是多少，按照上面的方法算一下，是5。

這就意味著，如果像剛才那樣右移一位的話，那str2相對于下標為10的前綴與后綴最大匹配長度應該為9，但是現在只有5，所以右移一位肯定不能和str1匹配。

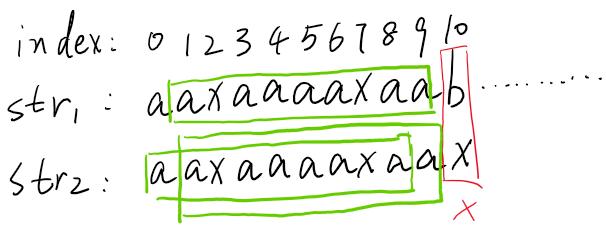
那么應該移動多少位呢？沒錯，就是5位。然后接著去匹配。

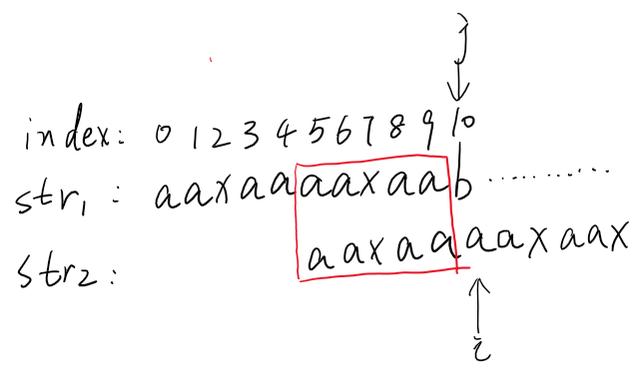
至此，關于KMP的大體思路已經講解完畢，接下來的關鍵就是如何求出一個字符串中對于所有位置的前綴與后綴最大匹配長度。也就是我們常說的next數組。

如何求next數組

我們人為規定了next[0]=-1和next[1]=0，即0位置的前綴與后綴最大匹配長度是-1，而1位置的前綴與后綴最大匹配長度是0.現在我們假設要求i位置的前綴與后綴最大匹配長度，而現在又知道i-1位置的前綴與后綴最大匹配長度為7，那么，如果j位置的字符和i-1位置的字符相等的話，就可以得到i位置的前綴與后綴最大匹配長度為7+1=8.

如果i-1位置的字符和j位置的字符不相等的話，而我們又知道j位置的前綴與后綴最大匹配長度為3，那么我們就去看看k位置的字符是否和i-1位置的字符相等，如果相等，則i位置的前綴與后綴最大匹配長度為3+1=4。如果不等，則再繼續以上操作，直到跳到0位置處，如果此時0位置還依然和i-1不等的話，那么i位置的前綴與后綴最大匹配長度為0。

以上這一段看著可能有點復雜，但是實際上很好理解，大家用紙和筆來畫一下就清楚了！

下面是求next數組的代碼

 	public static int getIndexOf(String s, String m) {
		if (s == null || m == null || m.length() < 1 || s.length() < m.length()) {
			return -1;
		}
		char[] str1 = s.toCharArray();
		char[] str2 = m.toCharArray();
		int i1 = 0;
		int i2 = 0;
		int[] next = getNextArray(str2); // O (M)
		// O(N)
		while (i1 < str1.length && i2 < str2.length) {
			if (str1[i1] == str2[i2]) {
				i1++;
				i2++;
			} else if (next[i2] == -1) { // str2中比對的位置已經無法往前跳了
				i1++;
			} else {
				i2 = next[i2];
			}
		}
		// i1 越界  或者  i2越界了
		return i2 == str2.length ? i1 - i2 : -1;
	}

利用next數組進行字符串匹配行為

按照以上的思路，我們就可以利用next數組去執行KMP算法了，最終我們是要得到str2在str1全匹配的str1的下標位置，以下圖為例，最終KMP算法是要返回8，因為str2是在str1的下標為8的位置處匹配上的，如果str2沒有被包含在str1中，那么返回-1.

下面是利用next數組進行KMP算法的代碼

public static int[] getNextArray(char[] ms) {
		if (ms.length == 1) {
			return new int[] { -1 };
		}
		int[] next = new int[ms.length];
		next[0] = -1;
		next[1] = 0;
		int i = 2; // next數組的位置
		int cn = 0;
		while (i < next.length) {
			if (ms[i - 1] == ms[cn]) {
				next[i++] = ++cn;
			} else if (cn > 0) { // 當前跳到cn位置的字符，和i-1位置的字符配不上
				cn = next[cn];
			} else {
				next[i++] = 0;
			}
		}
		return next;
	}