
二進制是計算機編碼、存儲和操作信息的核心,圍繞數值0和1的研究已經演化出了豐富的數學知識體系。這起源于1850年前后喬治•布爾(George Boole)的工作,布爾注意到將邏輯值True(真)和False(假)編碼為二進制值1和0,能夠設計出一種代數,以研究邏輯推理的基本原則。因此也稱為布爾代數(Boolean algebra)。
最簡單的布爾代數是在二元集合{0,1}基礎上的定義。下圖是這種布爾代數中的幾種運算。
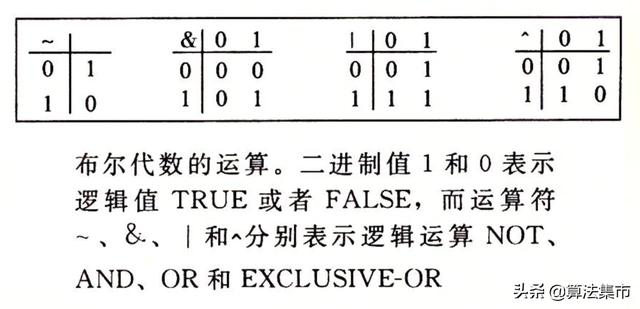
用來表示這些運算的符號與C語言位級運算使用的符號是相匹配的。
- 布爾運算 ~ 對應于邏輯運算:非 NOT。在命題邏輯中,當P等于0時,~P等于1,反之亦然。
- 布爾運算 & 對應于邏輯運算:且 AND。在命題邏輯中,當P=1且Q=1時,P&Q才等于1。
- 布爾運算 | 對應于邏輯運算符:或 OR。在命題邏輯中,當P=1或Q=1時,P|Q等于1。
- 布爾運算 ^ 對應于邏輯運算符 :異或。在命題邏輯中,當P=1且Q=0,或 P=0且Q=1時,P^Q等于1。
后來創立信息論的Claude Shannon首先建立了布爾代數和數字邏輯之間的聯系。他在1937年的碩士論文中表明了布爾代數可以用來設計和分析機電繼電器網絡。
C語言的一個很有用的特性就是它支持按位布爾運算,在布爾運算中使用的符號(~、&、|、^)能運用到任何整型的數據類型上。

確定一個位級表達式的結果的最好辦法就是將十六進制的參數用二進制表示再執行二進制運算,然后再轉回十六進制。






