
偉大的發現會成為未來的常識。
01
微積分的本質
“微積分的基本定理”是微積分的重要知識。打比方來說,這 就相當于金槍魚中珍貴的魚腩部分。高中的教科書里一般都會涉及 這方面的內容,比如“微分和積分互為逆運算”等。
這個表述確實沒有錯誤。如果說是否正確,那當然是對的。

“微分和積分互為逆運算”這句話表述有些過于簡潔,它具體的意思是什么呢?我非常希望大家能理解其本質。
大家是否曾覺得圓和球是相似的東西?關于圓和球存在以下 表述:
(1)“圓的面積”的微分就是“圓的周長”;
(2)“球的體積”的微分就是“球的表面積”。這些表述有些讓人摸不著頭腦,果真如此嗎?
(1)半徑為r的圓的面積是
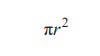
對r微分后得出
這與半徑為r的圓周長完全一樣。
(2)半徑為r的球的體積是
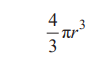
對r微分后得出
這是半徑為r的球的表面積。

(1)設半徑為r的圓(圓板)的面積是關于r的函數:
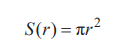
依照我們的老辦法,現在思考“圓的半徑增加Δr 時,面積會 增加多少”。
請觀察圖 95 中的大圓。圓的半徑增加Δr時,哪里會增加呢?增加的部分是薄圓環。這個環狀面積大致可以表示為:
圓的周長×Δr
即面積增加的部分(ΔS)為
ΔS ≈圓的周長×Δr
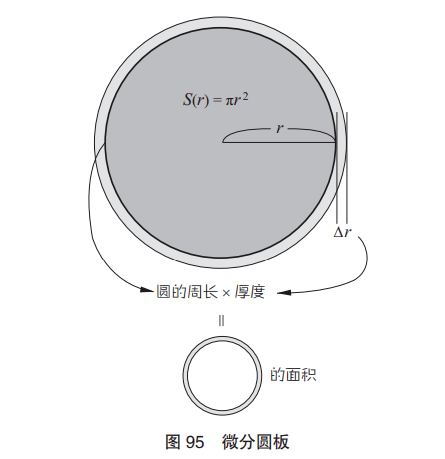
在這里,出現了一個符號“約等于”(≈)。因為外側圓的周長 稍微比內側圓的周長大一些。雖說有必要使用約等于號,但是總會 讓人覺得不嚴謹。如果可以的話,還是盡可能轉化為等號。
因此,首先將式子的兩邊除以Δr,因為

取Δ 0 r → 時
的極限。這樣一來,去掉“約”,即為
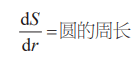
所以“圓的面積”的微分=“圓的周長”成立。
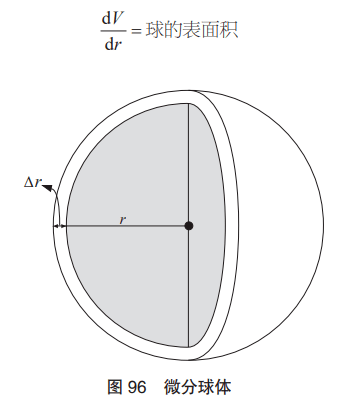
(2)我們用和(1)相同的思路來思考 “球的體積”的微分 = “球的表面積”。
半徑為r的球的體積為
與圓的情況一樣,我們來思考“球的半徑增加Δr時,體積會增加 多少”。
根據圖 96 可知,體積增加的部分是球外側很薄的那一部分皮。假設球為乒乓球,可以說增加的部分是用賽璐珞做成的部分(乒乓 球本身)。為了便于觀察,圖 96 中的球體增加了較為夸張的厚度。這層薄皮的體積大致為
球的表面積×Δr
也就是說,體積增加的部分ΔV為
和圓的做法一樣,兩邊除以Δr,取Δ 0 r → 時
的極限,得到
與剛剛的“圓的面積”的微分是“圓的周長”同理,可知“球 的體積”的微分=“球的表面積”成立。
根據以上證明可知,本節開篇所講(1)、(2)雖然讓人覺得不 可思議,但確實都是成立的。
實際上,這個關系就是“微積分的基本定理”。但是這其實是從不同的角度 講解了相同的內容。詳細來說即為以下內容。
第一,我們可以認為“圓面積的微分”最終就是(在使Δr 趨向于 0 的極限情況下)把圓分割成薄圓環狀。也就是說,粗略來講 的話,微分就是從圓板上多個同心圓之間排列的薄圓環中,取出 1 個薄圓環。另一方面,積分則是累加極薄圓環的面積從而求出圓的 面積(圖 97)。
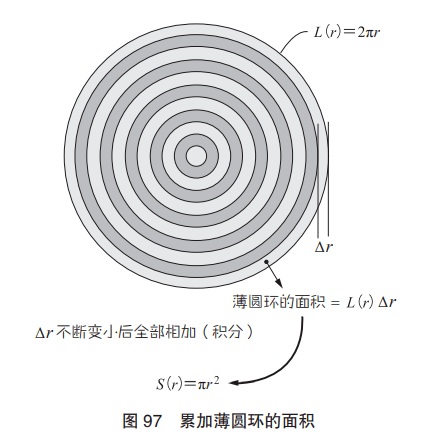
圓環的面積(≈ L( r)Δ r)等于圓的周長乘以Δr,累加所有圓環 面積就是圓的面積。所以圓的面積等于
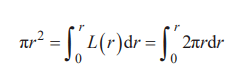
即
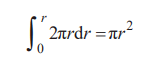
成立。將式子兩邊除以2π,得出
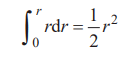
第二,關于球的內容,累加“表面積×Δr ”,就能求出球整體 的體積。所以
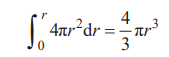
成立。
將式子兩邊除以4π,得出
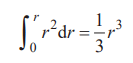
把微分公式
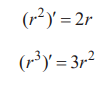
代入,得出積分公式
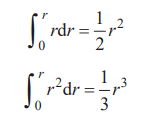
即“分割”成較小部分的操作是微分,相反,“累加”較小部分的 操作是積分(圖 98)。
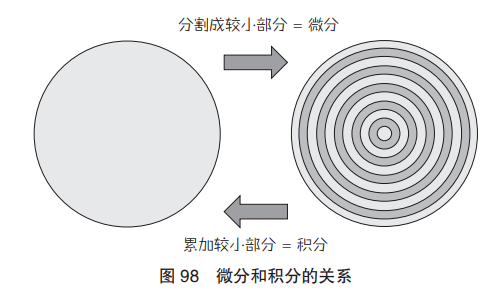
微分和積分就像硬幣的正反面,是完全相反的關系。
02
基本定理的使用方法
真正理解了“微積分的基本定理”,就會覺得這東西并不復雜。但是,這個定理的厲害之處在于應用范圍很廣。雖然看起來很普 通,但是很實用。
比如說“冪函數的微分公式”是
我們以此來嘗試推導“冪函數的積分公式”。
根據微積分的基本定理可知,冪函數的微分公式的意思可以用 圖 99 來表示。
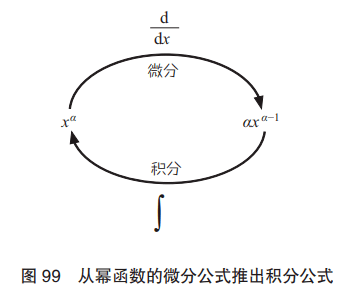
即冪函數的微分公式的意思是:
改變α的值就可以不斷列舉出:

把這些式子(也可以說是句子)依次分別除以 3、4,可以 得出:

積分式子即使無限地寫下去,其意思也十分簡單。
也就是說,一般“指數增加 1”后寫在分母和x的右上角,即
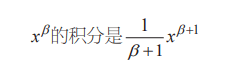
但是,有一點必須要注意。
實際上到目前為止,我們使用“積分”這個詞時,意思是有 些不清晰的。比如說,在剛剛解釋的冪函數中,微分
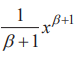
可以得到
但是,還存在其他函數,其微分結果也為
這里,我們漏掉 了微分得 0 的函數。問題就在于此。即如果將
微分的話,其結果也得
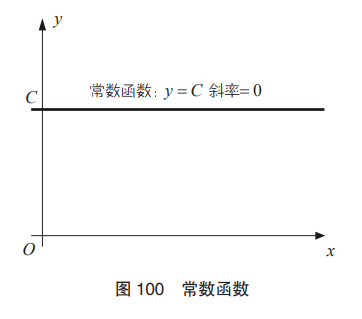
“微分得 0 的函數”也就是“沒有變化的函數”,這種函數叫作 “常數函數”。常數函數的斜率為 0,即對于任何 x 值函數的結果都 相同。設常數函數值為C,則可以寫成
如圖 100 所示,常數函數的函數值沒有變化。其中的常數C,可以 是 100,可以是 -50,也可以是 10 萬億。重要的是C“沒有變化”, 而不是數值本身是大是小。
這是冪函數的積分公式。
對f( x) 的微分進行積分得出的函數,叫作“f ( x) 的原函數”, 寫作F ( x),即
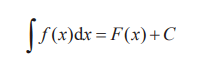
原函數中始終存在“一項不定數值 C(不定項)”。在這里,“通過 積分求出原函數”,這叫作不定積分。相反,像之前提到求取面積 或者體積的積分,叫作定積分。不定積分和定積分不同,原則上不 寫“從哪里到哪里的積分”。
多出的這個 C,就像多余的裝飾品讓人無法平靜,不過可以不 用在意。因為在計算面積等問題時,C 就會消失。
例如,圖 101 中灰色部分的面積,用定積分符號表示的話, 寫作
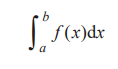
這個定積分的值為
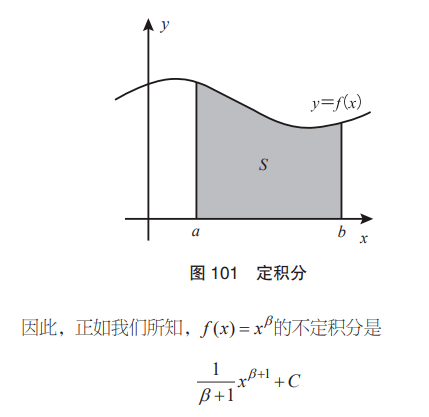
這里有一條向右上方傾斜 45°的直線y x = 。
從x =1到x = 2之 間的面積是多少(圖 102)?
因為灰色部分是梯形,所以可以用(上底 +下底) ×高 ÷ 2 的 公式計算面積。 圖中的梯形往左邊傾倒,上底的值為x =1時y的值, y = x=1。 下底也一樣,為x = 2時y的值,y = x= 2。 高是2 − 1= 1,所以面積是
另一方面,使用積分公式可得
這與梯形面積公式計算出來的結果完全相等。
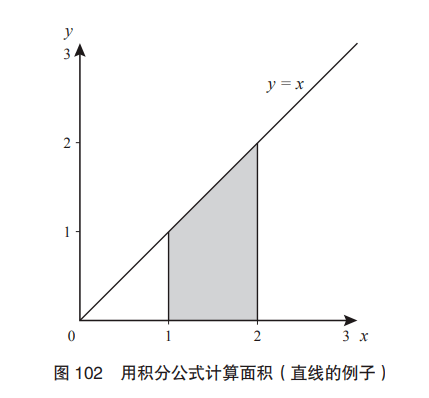
下面,我們來看拋物線的例子。
圖 103 是拋物線部分圖像。計算從x =1 到x = 2 的面 積。這次的圖無法再使用“梯形面積公式”,所以只能使用積分。
套用積分公式得出
看,一瞬間就可以得出答案。沒有積分似乎很難計算出來。不得不 說,積分真是太厲害了。
順便說一下,前文說到圓的面積、球的表面積時出現了公式
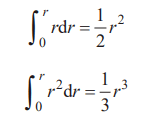
這里只是把x換成了r,是冪函數的積分公式的特殊情況(分別為β =1、β = 2)。
03
近似和忽略
微積分的本質在于近似與忽略。近似指的是忽 略一些東西,只給出大概的答案。
即使是復雜的形狀,也可以將其視為簡單長方形的組合(積 分),函數在局部可以視為切線或者拋物線(微分),這個思考角度 才是微積分的要領。
重要的是不要在意細節。不在意細小的部分,“用直線段近似 函數圖像”就可以搞清楚容積最大的冰激凌蛋卷筒是什么形狀,也可以“把曲線看作折線的組合”來計算懸鏈線的長度。雖然整體計算很難,但分成較小的部分就會變成簡單的累加。這就是微積分厲害之處。
實際上,這種思想并不僅限于微積分,可以說整個數學都是這樣的。微積分則是了解該方法有效性的最好素材。
實際上,我們居住的現實世界中,近似可以說是無處不在。比如,不存在無限小的東西(無法比基本粒子更小),宇宙也并非無限廣闊。
但是,在實際的微積分中,要考慮無限小的量,或者無限大的空間,這是近似。忽略基本粒子的大小,擱置宇宙的邊界限制,這種想法或許與事實相悖,但是這種方法給我們帶來的恩惠卻不可估量。
微分積分的內容是從細致分割圖形開始講起的,之后又講到自然常數e,最后又到懸鏈線的長度。讀到這里,大家是不是已經自然而然地認可“近似和忽略”的思考方法呢?如果是的話,那么這就是很大的進步了。

《簡單微積分:學校未教過的超簡易》
作者:[日]神永正博
譯者:李慧慧
僅用“閱讀”就能理解微積分原理,無須背誦公式、煩瑣計算,傳授日本微積分入門的“巧妙思路”。
書為微積分入門科普讀物,書中以微積分的“思考方法”為核心,以生活例子通俗講解了微積分的基本原理、公式推導以及實際應用意義,解答了微積分初學者遭遇的常見困惑。

《微積分的歷程:從牛頓到勒貝格》
作者:鄧納姆
譯者:李伯民 汪軍 張懷勇
本書榮獲“第七屆文津圖書獎推薦書目”。
這不是一本數學家的傳記,而是一座展示微積分宏偉畫卷的陳列室。書中的每一個結果,從牛頓的正弦函數的推導,到伽瑪函數的表示,再到貝爾的分類定理,無一不處于各個時代的研究前沿,至今還閃爍著耀眼奪目的光芒。

《普林斯頓微積分讀本(修訂版)》
《普林斯頓數學分析讀本》
《普林斯頓概率論讀本》
作者:[美] 史蒂文·J. 米勒、拉菲·格林貝格、史蒂文·J. 米勒
譯者:李馨
風靡美國普林斯頓大學的數學課程讀本,教你怎樣在數學考試中獲得高分,用大量例子和代碼全面探討數學問題提供課程視頻和講義。被譽為“普林斯頓讀本”三劍客。

《微積分溯源:偉大思想的歷程》
作者:戴維·M. 布雷蘇
譯者:陳見柯 林開亮 葉盧慶
從古希臘、古埃及、古印度、中國和歐洲等地的微積分思想,到牛頓、萊布尼茨、伯努利兄弟、黎曼等偉大數學家的輝煌成就,看一看微積分這座“數學寶藏”是如何被塑造成今天的模樣的。






