對稱建筑
我想每個人都知道對稱是什么。但是你知道嗎，自然定律也是對稱的。
每個人都知道圖一左邊的墨跡是對稱的，但很少有人知道右邊圖形在精確的數(shù)學(xué)意義上也是對稱的。
那么，什么是對稱性呢?為什么這個概念變得如此重要，以至于許多科學(xué)家認(rèn)為它是自然法則的基礎(chǔ)?
圖一
關(guān)于對稱
對稱表示對可能的變化免疫——那些頑固的形狀、短語、定律或數(shù)學(xué)表達式的核心，在某些變換下保持不變。
例如，讀一下短語“上海自來水來自海上”，當(dāng)從后往前讀時，它是對稱的。也就是說，當(dāng)?shù)怪x的時候，句子是完全一樣的。
這樣的例子很多，具有這種對稱性的短語被稱為回文。而且這樣的對稱在男性定義的Y染色體結(jié)構(gòu)中起著重要作用。
對稱在基因中
直到2003年，基因組生物學(xué)家認(rèn)為，由于Y染色體缺少一個伴侶(可以與之交換基因)，它的基因載體將通過破壞性的突變逐漸減少。
然而，令他們驚訝的是，對Y染色體進行測序的研究人員發(fā)現(xiàn)，它通過“回文”來抵抗破壞。
在5000萬個染色體的DNA字母中，大約有600萬個形成回文序列。這些“鏡像”拷貝在破壞性突變的情況下提供備份，并在某種意義上允許染色體與自身交配，因為可以互換位置。
圖二：蝴蝶（左）和雪花（右）
對稱圖形
對于二維圖形和形狀，比如那些畫在紙上的圖形，有四種“剛性”對稱(當(dāng)不允許拉伸和變形時)，為反射、旋轉(zhuǎn)、平移和滑動反射。
我們在周圍的反射下遇到對稱，這是我們熟悉的動物的兩側(cè)對稱。在圖二中蝴蝶(左)的中間畫一條線。現(xiàn)在把它翻轉(zhuǎn)過來，同時保持中心線的位置。由此產(chǎn)生的完美重疊表明蝴蝶在其中心線的反射下保持不變。
旋轉(zhuǎn)下的對稱性在自然界中也很普遍。圖二雪花(右)旋轉(zhuǎn)60度、120度、180度、240度、300度或360度，繞著一個軸(垂直于它的平面)旋轉(zhuǎn)，是完全重合的。
平移是指沿著一條特定的直線移動一定距離，圖形依然能夠重疊。許多古典的中楣、墻紙設(shè)計、高層公寓的一排排窗戶，甚至蜈蚣，都表現(xiàn)出這種對稱。
最后，行走中產(chǎn)生的腳印在滑動反射下是對稱的(圖三)。在這種情況下，轉(zhuǎn)換包括平移(或滑動)，然后是平行于位移方向的線（虛線）中的反射。
圖三
到目前為止討論的所有對稱都是圖形和形式的對稱，我們可以用眼睛看到。自然基本定律背后的對稱性在某種意義上與這些定律密切相關(guān)，但它們并沒有把重點放在形式或圖形上，而是解決了一個不同的問題:
在我們周圍的世界上，可以進行哪些變化，使描述所有觀察到的現(xiàn)象的定律保持不變?
對稱規(guī)則
“自然定律”概括地描述了一系列規(guī)則，這些規(guī)則被認(rèn)為可以從字面上解釋我們在宇宙中所觀察到的一切。
這樣一套宏大的規(guī)則在17世紀(jì)之前是不可想象的。只有通過像伽利略(1564-1642)、勒內(nèi)·笛卡爾(1596-1650)，特別是艾薩克·牛頓(1642-1727)這樣的科學(xué)巨人的著作，人們才清楚地認(rèn)識到，僅僅幾個定律就可以解釋廣泛的現(xiàn)象。
突然之間，各種各樣的事情，如蘋果落下，海灘上的潮汐，行星的運動，都落在牛頓萬有引力定律的范圍里。
同樣，基于邁克爾·法拉第(1791-1867)的實驗結(jié)果，蘇格蘭物理學(xué)家詹姆斯·克拉克·麥克斯韋(1831-1879)只用四個方程就能解釋所有經(jīng)典的電、磁和光現(xiàn)象!
能想象嗎，整個電磁學(xué)的世界用四個方程表示。
可觀測宇宙
自然定律被發(fā)現(xiàn)遵循著一些我們已經(jīng)遇到過的相同的對稱，以及一些其他的，更深奧的對稱。
首先，這些定律在平移時是對稱的。這個特性的表現(xiàn)很簡單:無論你在北京或上海，在銀河系的另一端，還是在10億光年外的星系中進行實驗，你都可以用同樣的定律來描述結(jié)果。
我們怎么知道這是真的?因為對宇宙中所有星系的觀察表明，不僅引力定律一樣，而且可觀測宇宙邊緣的氫原子遵循的電磁學(xué)和量子力學(xué)定律與它們在地球上遵循的定律完全相同。
自然定律在旋轉(zhuǎn)方面也是對稱的，無論我們測量的方向是北方還是最近的咖啡店，這些定律都完全一樣——物理學(xué)在空間中沒有首選的方向。
如果沒有這種在平移和旋轉(zhuǎn)下的驚人的定律對稱性，就沒有希望理解宇宙的其他部分。此外，即使在地球上，如果定律不是對稱的，實驗也必須在全球每個實驗室重復(fù)進行。
需要一個謹(jǐn)慎的詞來區(qū)分形狀的對稱性和規(guī)律的對稱性。古希臘人認(rèn)為行星圍繞太陽的軌道是絕對圓形。事實上，并不是軌道形狀，而是牛頓引力定律在旋轉(zhuǎn)下是對稱的。
這意味著軌道可以是橢圓的(而且確實是橢圓的!)，但是軌道在空間中可以有任何方向。
在開篇就說過，對稱性可能是定律的來源。這是什么意思?
圖四：雪花（左）和行星運動軌道（右）
自然定律的來源
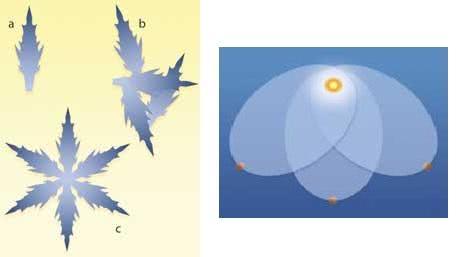
假設(shè)你從來沒有聽說過雪花，有人讓你猜一猜雪花的形狀。顯然，這是一項不可能完成的任務(wù)。你可能會覺得，雪花可能看起來像土豆，像水壺，或者像怪羅科普。
即使已知雪花的一點形狀(圖四左.a)，并被告知這是雪花整體形狀的一部分，你還時不可能猜測到，雪花仍然可以有很多形狀（圖四左.b）。
另一方面，如果你被告知，雪花在圍繞其中心旋轉(zhuǎn)60度的情況下是對稱的，這個信息非常有用。這種對稱性立即將可能的構(gòu)型限制為6個角、12個角、18個角，以此類推。
假設(shè)，根據(jù)經(jīng)驗，大自然會選擇最簡單，最經(jīng)濟的解決方案，一個六角雪花(圖四左.c)將是一個非常合理的猜測。
換句話說，對形狀對稱性的要求引導(dǎo)我們朝著正確的方向前進。
同樣，要求自然定律在某些變換下是對稱的，這不僅規(guī)定了這些規(guī)律的形式，而且在某些情況下，還需要存在力或尚未發(fā)現(xiàn)的基本粒子。讓我用兩個有趣的例子來解釋。
愛因斯坦
愛因斯坦解釋廣義相對論的主要目標(biāo)之一是建立一個理論，在這個理論中，自然法則在所有觀察者看來都是完全相同的。
也就是說，在我們時空觀點的任何變化下，定律必須是對稱的 (在物理學(xué)中，這被稱為“一般協(xié)方差”)。
坐在巨龜背上的觀察者，應(yīng)該能推導(dǎo)出與坐在旋轉(zhuǎn)木馬或加速火箭上的觀察者相同的定律。事實上，如果這些定律是普遍的，那么它們?yōu)槭裁匆Q于觀察者是否在加速呢?
每當(dāng)一架飛機撞上一個氣囊，我們就會感到我們的胃跳到了喉嚨里——在勻速運動和加速運動之間似乎有著明顯的區(qū)別。那么，對于加速觀察者來說，當(dāng)這些觀察者似乎經(jīng)歷了額外的力時，自然定律如何能夠相同呢?
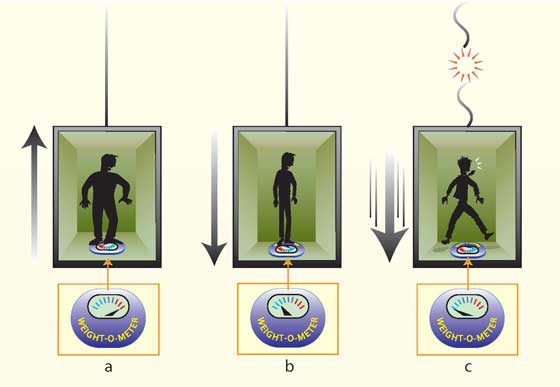
圖五
考慮以下情況，如果你站在向上加速的電梯里的秤上，你的腳會對秤施加更大的壓力——秤的重量會更重(圖五.a)。如果是向下加速的電梯會感覺到重力較弱(圖五.b)。如果電梯的電纜斷開，您和秤將一起自由下落，并且秤將記錄為零重量（圖五.c）。
自由落體相當(dāng)于人奇跡般地失去重力。這使得愛因斯坦1907年開創(chuàng)性的結(jié)論:重力和加速度所帶來的力實際上是一回事。
這種強大的統(tǒng)一被稱為“等效原理”，這意味著加速度產(chǎn)生的力和重力實際上是同一力的兩個方面。
1922年在京都的一次演講中，愛因斯坦描述了他1907年頓悟的那一刻:“我坐在伯爾尼的專利局里，突然想到:如果一個人自由落體，他不會感覺到自己的體重。我被嚇了一跳。這個簡單的想法給我留下了深刻的印象。它促使我走向萬有引力理論。”
等效原理實際上就是一種普遍對稱的表述;自然定律由愛因斯坦的廣義相對論方程表達，在所有系統(tǒng)中都是相同的，包括加速系統(tǒng)。
那么，為什么在旋轉(zhuǎn)木馬和靜止的實驗室中觀察到的結(jié)果有明顯的不同呢?廣義相對論給出了一個答案。它們只是環(huán)境上的差異，而不是定律本身的差異。
同樣，由于地球的引力，上下方向在地球上看似不同。自然定律本身沒有偏好的方向，它們在旋轉(zhuǎn)下也是對稱的，它們不區(qū)分上下。
根據(jù)廣義相對論，旋轉(zhuǎn)木馬上的觀察者感受到的離心力相當(dāng)于重力。在時空坐標(biāo)的任何變化下，定律的對稱性需要存在引力！對稱的要求讓大自然別無選擇:重力必須存在。
好了！現(xiàn)在對稱更深層次的作用了吧！
快速閱讀
1、關(guān)于對稱：對變化的免疫
2、對稱在基因中：Y染色體的“回文對稱”來抵抗破壞性
3、對稱規(guī)則：分為反射、旋轉(zhuǎn)、平移和滑動反射對稱
4、通過可觀測宇宙的觀察表明，自然定律的性質(zhì)和圖形的對稱存在相同的特性，所以說自然定律具有對稱性
5、自然定律的來源：形狀對稱性的要求引導(dǎo)我們朝著正確的方向前進
6、因為對稱性，推出引力必須存在（萬有引力）
