K-最近鄰算法（K-Nearest Neighbor，KNN）是一種經(jīng)典的有監(jiān)督學(xué)習(xí)方法，也可以被歸為懶惰學(xué)習(xí)（Lazy Learning）方法。它基于“物以類聚”的原理，假設(shè)樣本之間的類別距離越近則它們越有可能是同一類別。
KNN算法的工作原理簡單且直觀，當需要將一個測試樣本分類時，它首先會計算測試樣本與所有訓(xùn)練樣本之間的距離，然后根據(jù)距離的遞增關(guān)系進行排序。接著，它會選擇距離最小的前K個樣本，并統(tǒng)計這K個最近鄰樣本中每個樣本出現(xiàn)的次數(shù)。最后，它會選擇出現(xiàn)頻率最高的類標號作為未知樣本的類標號。
在KNN算法中，K值的選擇是關(guān)鍵。如果K值較小，只有當需要進行預(yù)測的樣本和訓(xùn)練的樣本較接近時，才能有較好的效果。如果K值較大，則算法分類的近似誤差增大，與輸入樣本距離較遠的樣本也會對結(jié)果產(chǎn)生作用。
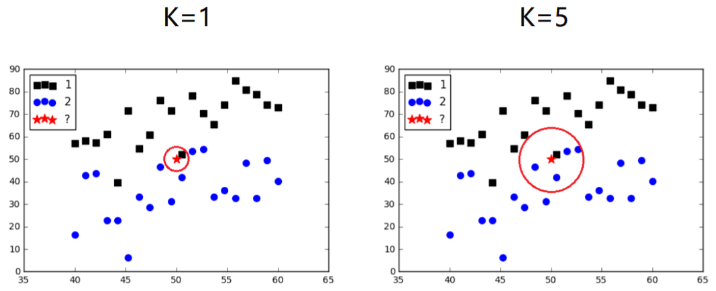
KNN算法的工作過程如下：
1. 計算待分類樣本與訓(xùn)練集中所有樣本之間的距離，常用的距離度量方法包括歐氏距離、曼哈頓距離等。
2. 選擇K個距離最近的樣本，即K個最近鄰。
3. 對于分類問題，統(tǒng)計K個最近鄰中不同類別的樣本數(shù)量，并將待分類樣本歸為數(shù)量最多的那個類別。
4. 對于回歸問題，計算K個最近鄰的平均值或加權(quán)平均值，并將其作為待分類樣本的預(yù)測值。
KNN算法的優(yōu)點是簡單易理解、實現(xiàn)容易，并且對于非線性問題具有較好的表現(xiàn)。此外，KNN算法可以適應(yīng)新的訓(xùn)練數(shù)據(jù)，不需要重新訓(xùn)練模型。KNN算法既能夠用來解決分類問題，也能夠用來解決回歸問題。在處理分類問題時，KNN通過掃描訓(xùn)練樣本集找到與測試樣本最相似的訓(xùn)練樣本，并依據(jù)該樣本的類別進行投票確定測試樣本的類別。在處理回歸問題時，KNN則通過計算訓(xùn)練樣本與測試樣本的相似程度進行加權(quán)投票。
然而，KNN算法的缺點包括計算復(fù)雜度高，需要存儲全部訓(xùn)練樣本，對于大規(guī)模數(shù)據(jù)集會消耗較多的內(nèi)存和時間。此外，KNN算法對于樣本分布不平衡的情況可能產(chǎn)生偏見，并且對于高維數(shù)據(jù)和噪聲數(shù)據(jù)的處理能力相對較弱。
需要注意的是，由于KNN算法需要計算所有訓(xùn)練樣本與測試樣本之間的距離，因此當訓(xùn)練樣本集較大時，其計算成本會較高。為了解決這個問題，可以考慮使用一些優(yōu)化的距離計算方法，如樹結(jié)構(gòu)算法等。同時，KNN算法的方差（Variance）往往較高，容易受到訓(xùn)練集大小和噪聲的影響，因此在使用時需要注意過擬合和欠擬合的問題。
在應(yīng)用方面，KNN算法常用于推薦系統(tǒng)、圖像識別、醫(yī)學(xué)診斷等領(lǐng)域。
