
圖片來源@視覺中國
文 | 追問NextQuestion
大腦是宇宙中已知的,也可能是唯一的“智能機器”。
在行為學層面,人與動物的大腦能執(zhí)行精細的、高水平的認知任務,包括靈活學習、長時程記憶、開放式環(huán)境決策等。在結構層面,認知與計算神經科學揭示了大腦通過極其復雜而精細的網絡實現其功能。北京大學心理與認知科學學院吳思教授與清華大學社會科學院心理學系的劉嘉教授等人在今年1月發(fā)表的“AI of Brain and Cognitive Sciences: From the Perspective of First Principles”一文中提到,隨著人類對大腦的結構與功能的認識不斷深化,大腦的基本原理為改進人工智能提供了最重要的參考。這些基本原理指大腦提取、表征、處理、檢索信息的規(guī)則,它們指引著大腦的運行,是大腦執(zhí)行其他更高級認知功能的基礎。
論文作者們將大腦的基本原理概括為:吸引子網絡、臨界性、隨機網絡、稀疏編碼、關系記憶、感知學習。解讀這些原理,并將其靈活用于人工智能,可能是使人工智能更“像”人類智能,并在性能上獲得進一步提升的關鍵。
本次追問邀請了四位認知神經科學領域的青年學者基于這篇重要論文對“人工智能如何向人類智能學習?”的話題進行了解讀。本次解讀將分上中下三篇,從以上六個方面與您一起揭秘大腦的基本原理。

?圖 1:論文封面
吸引子動力學:神經信息處理的規(guī)范模型
大腦由大量神經元組成,神經元之間通過突觸形成各種網絡。單個神經元的計算相當簡單,而神經網絡的動態(tài)變化才是完成大腦功能的關鍵。簡單地說,神經網絡接收來自外部世界和其他腦區(qū)的輸入,其狀態(tài)不斷變化,從而進行信息處理。因此,動態(tài)系統理論是量化大腦如何通過網絡進行計算的重要數學工具。
在動力學系統中,不同的狀態(tài)演化規(guī)則和多樣的外部輸入可以產生各種動態(tài)學現象。在一個神經網絡里,如果一個狀態(tài)向量(state vector)的所有鄰近狀態(tài)都匯聚于它,那么這個狀態(tài)向量就被稱為穩(wěn)定吸引子(stable attractor)。擁有穩(wěn)定吸引子的網絡被稱為吸引子網絡(attractor.NETwork),它們構成了大腦信息表征、處理和檢索的基本構建模塊。具有穩(wěn)定狀態(tài)的吸引子網絡可分為兩種類型,即離散吸引子網絡(discrete attractor network)和連續(xù)吸引子網絡(continuous attractor network)。在神經網絡中,吸引子對應網絡的能量空間中的局部最小值,所有鄰近狀態(tài)的能量都高于它,所以會被“吸引”到這里(圖1)。
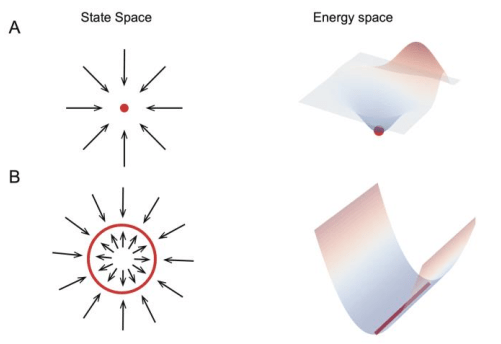
?圖 1:離散吸引子網絡和連續(xù)吸引子網絡示意圖。圖源:參考文獻1
在離散吸引子網絡中,每個吸引子都有自己的吸引區(qū)域。如果以隨機狀態(tài)開始,網絡的動態(tài)性會驅動隨機狀態(tài)向其鄰近吸引子狀態(tài)變化,這個過程也伴隨著網絡的能量降低。離散吸引子的這種特性使得網絡能夠糾正輸入噪聲并檢索記憶表征。現在,離散吸引子網絡經常用于模擬工作記憶、長期記憶和決策等。
與離散吸引子網絡不同,在連續(xù)吸引子神經網絡(continuous attractor neural networks,CANN)中,吸引子在狀態(tài)空間中連續(xù)分布,形成一個平滑的流形。這個特性使得CANN中的吸引子狀態(tài)能夠迅速轉變。它為CANN帶來了許多潛在的利用價值,如路徑積分、證據累積、預測性跟蹤等。
已經有很多實驗研究證明大腦中存在吸引子動力學,并且吸引子網絡常被用于描述一些高級認知功能的潛在機制,這有賴于其在信息表征中的基本特性。
- 特征一:吸引子網絡穩(wěn)健的信息表征2
在離散吸引子網絡中,記憶信息被存儲為一個吸引子狀態(tài)。在給定部分或有噪聲線索的情況下,網絡會動態(tài)演化到一個吸引子狀態(tài),并且相應的記憶會被檢索出來。不同的吸引子對應于不同的局部能量最小值,并且有著各自的吸引域。如果噪聲擾動不足以將網絡狀態(tài)推出吸引域,那么吸引子狀態(tài)就是穩(wěn)定的,所以記憶信息被穩(wěn)健地編碼。
與離散吸引子網絡不同,在連續(xù)吸引子網絡中,吸引子在網絡狀態(tài)空間中形成一個平坦的流形,并且它們對噪聲有部分的穩(wěn)健性。如果噪聲擾動與流形正交,網絡狀態(tài)在吸引子動力學作用下是穩(wěn)定的。然而,如果噪聲擾動沿著流形方向,網絡狀態(tài)將在吸引子流形上擴散,從一個吸引子移動到附近的吸引子。
- 特征二:吸引子網絡的記憶容量
記憶容量指的是能夠可靠地存儲在吸引子網絡中的記憶數量。吸引子網絡的記憶容量受到幾個因素的影響。其一是噪聲,當網絡中存儲了過多的記憶時,每個吸引子的吸引域會縮小,從而降低了吸引子對噪聲的容忍度。另一個因素是記憶相關性,當記憶模式高度相關時,它們會相互干擾,破壞記憶的檢索。為了增加吸引子網絡的記憶容量,人們已經提出了許多方法,從學習規(guī)則到網絡結構,如基于新奇性的赫布規(guī)則(Hebbian rule)3和模塊化霍普菲爾德網絡(Hopfield network)4。
- 特征三:吸引子網絡的信息檢索
除了具有大容量的記憶能力外,一個優(yōu)秀的信息處理系統還需要高效的信息搜索能力。在吸引子網絡中,記憶通常以內容尋址方式進行檢索,即網絡通過吸引子動態(tài)執(zhí)行相似性計算,檢索出與線索最相似的記憶。
在大容量網絡中,從眾多吸引子中找到正確的一個是具有挑戰(zhàn)性的。例如,在一個自由記憶檢索任務中,參與者需要盡可能多地搜索和回憶動物的名稱。一個良好的回憶策略是在局部記憶搜索與記憶空間大跳躍之間合適地組合,表現出萊維飛行行為*。董行思等人證明,在一個帶有噪聲神經適應的CANN中,網絡狀態(tài)的動態(tài)顯示出交替的局部布朗運動和長跳躍運動,呈現出萊維飛行的最佳信息搜索行為5。
*編輯注:萊維飛行行為(Levy flight behavior)是一種隨機行為模式,其中個體在一定時間內以不規(guī)則的方式移動,具有長尾分布的步長。這種行為模式以法國數學家Paul Lévy的名字命名。萊維飛行行為與傳統的隨機行走模型(如布朗運動)不同,后者通常假設步長是固定的,而萊維飛行行為中的步長是從長尾分布中隨機抽取的,因此具有更大的變化范圍。
- 特征四:吸引子網絡間的信息整合
吸引子網絡還可以相互交互,實現信息整合。張文昊等人研究了如何通過相互連接的CANN來實現多感官信息處理6, 7。在他們的模型中,每個模塊包含兩組神經元,每組神經元形成一個CANN,這些神經元的調諧函數相對于模態(tài)輸入要么是一致的,要么是相反的。該研究證明,具有一致神經元的耦合CANN可以實現信息整合,而具有相反神經元的耦合CANN可以實現信息分離,它們之間的相互作用能夠有效地實現多感官整合和分離。這項研究表明,相互連接的吸引子網絡可以支持不同腦區(qū)之間的信息傳遞。
最近,在全球范圍內的技術進步和大型腦項目的推動下,大量關于腦結構細節(jié)和神經活動的數據正在涌現,現在是建立大規(guī)模網絡模型來模擬更高級認知功能的時機。作為神經信息處理的規(guī)范模型,吸引子網絡成為人們開展這一任務的基本構建模塊,人工智能也可以借助這一基本模塊,在信息處理和表征方面受到一些啟發(fā)。
根據全局工作空間理論(global neuronal workspace theory)*,大腦分為一個共享的全局處理模塊和許多分布式的專門處理模塊8。每個獨特的模塊處理來自一個模態(tài)(如視覺、聽覺、嗅覺或運動系統)的信息。相反,全局模塊接收并整合來自所有專門模塊的信息,并將整合后的信息“廣播”回這些局部模態(tài)。為了實現這個目標,需要一個抽象的信息表示接口,允許不同模塊之間進行通信。從這個意義上說,已經在實驗和理論研究中被證明是規(guī)范模型的CANN,自然地成為了在模塊之間表示、轉換、整合和廣播信息的統一框架。在未來的研究中,探索這個問題將是非常有趣的。
*編輯注:全局工作空間理論或全局工作空間模型是1988年心靈哲學家巴爾斯(B. J. Baars)首次提出的運用語境論解釋意識運行的基本規(guī)則的模型。假設意識與一個全局“廣播系統”相聯系,該系統在整個大腦中發(fā)布信息,包括三個部分:專門處理器、全局工作空間和語境。專門處理器是無意識的,可能是一個單一的神經元,也可能是整個神經網絡。
臨界性:為大腦和人工智能帶來新的視角
臨界性(criticality)的框架是理解和分析復雜系統的強大工具,因為許多物理和自然系統處于臨界狀態(tài)。在過去的20年里,研究人員發(fā)現大腦中的生物神經網絡的運行接近臨界狀態(tài),這為研究腦部動態(tài)提供了新的視角。已知臨界狀態(tài)對腦部的活動/功能非常重要,因為它優(yōu)化了信息傳輸、存儲和處理的許多方面。在人工智能領域,臨界狀態(tài)的框架被用于分析和指導深度神經網絡的結構設計和權重初始化,表明運行接近臨界狀態(tài)可被視為神經網絡計算的基本原則之一。
在統計物理學中,一個具有相同物理和化學特性的材料系統中的均質狀態(tài)被稱為相(phase)。例如,水可以處于固相、液相或氣相。當溫度變化時,水可以從一個相變?yōu)榱硪粋€相,這被稱為相變(phase transition)。臨界狀態(tài)表明系統正在從有序相向無序相轉變。在有序和無序的邊緣,或者稱為“混沌邊緣”,臨界狀態(tài)表現出許多特殊的屬性。

?圖 2:蒙特卡洛模擬伊辛模型。圖源:參考文獻9
圖2通過伊辛模型的模擬展示了鐵磁材料的相變過程和臨界狀態(tài)9。在伊辛模型中,自旋相互作用和熱運動的競爭導致了有序相和無序相。圖2a和2c分別顯示了低溫下的有序相和高溫下的無序相。在相變邊緣的溫度下,如圖2b所示,有序和無序處于平衡狀態(tài),兩者都無法主導整個系統。在這個溫度下,系統變得極其復雜,處于所謂的臨界狀態(tài)。
在有序相或無序相中,領域大小的分布集中在較大或較小的尺寸上,而在臨界狀態(tài)下,領域大小幾乎分布在所有尺寸上。而且不同尺度上的分布是自相似的,這意味著這些分布是分形和無標度的。這種自相似分布在數學上可形式化為冪律(power law)10:
![]()
。如果使用對數-對數坐標系,分布將呈現為一條直線。冪律分布是臨界狀態(tài)的一個重要特征。
除了通過精確調節(jié)伊辛模型中的溫度或其他系統中的控制參數來達到臨界狀態(tài)外,有些系統還能自發(fā)地達到臨界狀態(tài),這被稱為自組織臨界性(self-organized criticality,SOC)。在過去的二十年中,通過記錄體外培養(yǎng)的腦組織或體內完整大腦的神經元活動,許多實驗表明大腦皮層網絡也能夠自組織成臨界狀態(tài)。
在大腦的皮層網絡中,每個神經元通過突觸連接接收來自大量周圍神經元的輸入。當輸入達到其閾值時,將產生動作電位,該電位將傳遞給其他神經元,導致其他神經元發(fā)放動作電位。Beggs和Plenz通過多電極陣列記錄大腦組織的活動首次確認了關于臨界大腦的猜測11。他們發(fā)現神經元雪崩的大小和持續(xù)時間都服從冪律分布,這是臨界狀態(tài)的一個重要特征。隨后,其他研究人員記錄了不同物種的不同腦皮層在清醒和麻醉狀態(tài)下的神經元活動,都再次證實了在網絡的自發(fā)活動中神經元雪崩呈冪律分布12。這表明,大腦網絡在臨界狀態(tài)附近運行是一個普遍特征,而興奮性和抑制性的平衡在維持臨界狀態(tài)方面起著關鍵作用。
鑒于臨界狀態(tài)在包括神經系統在內的許多復雜系統分析中的成功應用,一些研究人員還嘗試將臨界狀態(tài)應用于研究人工神經網絡,例如,改進儲層計算和增強深度神經網絡的性能。
儲層計算(reservoir computing,RC)通常指的是遞歸神經網絡(recurrent neural network,RNN)的一種特殊計算框架,其中可訓練的參數僅存在于最終的輸出層,即非遞歸的輸出層,而所有其他參數則是隨機初始化并在后續(xù)計算中保持固定狀態(tài)。目前,RC模型已成功應用于許多計算問題,例如時序模式分類、識別、預測和動作序列控制等任務。RC模型僅在網絡處于臨界狀態(tài)時表現良好,有時也被稱為“回聲狀態(tài)(echo state)”。受生物神經網絡中的短時突觸可塑性(short-term synaptic plasticity,STP)的啟發(fā),曾冠雄等人在RC模型中實現了一種SOC方案,通過短時抑制(short-term depression,STD)來調整RNN的狀態(tài),使其接近臨界狀態(tài)13。STD大大增強了神經網絡的穩(wěn)健性,使其能夠適應長期的突觸變化,同時保持由臨界狀態(tài)賦予的最佳性能。它還提示了大腦在不同時間尺度上組織可塑性的潛在機制,在允許用于學習和記憶所需的內部結構變化的同時,維持信息處理的最佳狀態(tài)(臨界狀態(tài))。
除此之外,臨界狀態(tài)對于增強深度神經網絡的性能也有啟示作用。深度神經網絡相較于淺層網絡取得了巨大的成功。為了在理論上解釋這一現象,Poole等人將黎曼幾何與高維混沌的均場理論相結合,揭示出深度隨機網絡中逐漸增加的深度與混沌狀態(tài)(臨界狀態(tài))的瞬時變化之間存在指數級表達能力的關系14。此外,他們證明這個特性在淺層網絡中是不存在的。這一發(fā)現對網絡的結構設計具有重要意義,為現有深度神經網絡的卓越性能提供了理論基礎。但是,目前關于臨界狀態(tài)是否總是有益的問題仍然是一個未解之謎。
臨界狀態(tài)為人們研究生物和人工神經網絡提供了一種全新的視角。目前,臨界性的框架不僅被用于理解神經動態(tài)和腦部疾病,還被用于分析深度神經網絡的運行并指導進一步的改進設計。在更好地理解應用于人工神經網絡的約束條件,以及設計更好的體系結構和動態(tài)規(guī)則來提高人工神經網絡在復雜信息處理中的性能方面,臨界性的框架將發(fā)揮更加重要的作用。
未完待續(xù)......
參考文獻:
- 1. Luyao Chen, Z.C., Longsheng Jiang, Xiang Liu, Linlu Xu, Bo Zhang, Xiaolong Zou, Jinying Gao, Yu Zhu, Xizi Gong, Shan Yu, Sen Song, Liangyi Chen, Fang Fang, Si Wu, Jia Liu, AI of Brain and Cognitive Sciences: From the Perspective of First Principles. arXiv, 2023. 2301.08382.
- 2. Lim, S. and M.S. Goldman, Balanced cortical microcircuitry for maintaining information in working memory. Nat Neurosci, 2013. 16(9): p. 1306-14.
- 3. Blumenfeld, B., et al., Dynamics of memory representations in networks with novelty-facilitated synaptic plasticity. Neuron, 2006. 52(2): p. 383-94.
- 4. Liu, X., et al., Neural feedback facilitates rough-to-fine information retrieval. Neural Netw, 2022. 151: p. 349-364.
- 5. Xingsi Dong, T.C., Tiejun Huang, Zilong Ji, Si Wu, Noisy Adaptation Generates Lévy Flights in Attractor Neural Networks. Advances in Neural Information Processing Systems, 2021. Dec 6;34:16791-804.
- 6. Zhang, W.H., et al., Decentralized Multisensory Information Integration in Neural Systems. J Neurosci, 2016. 36(2): p. 532-47.
- 7. Zhang, W.H., et al., Complementary congruent and opposite neurons achieve concurrent multisensory integration and segregation. Elife, 2019. 8.
- 8. Mashour, G.A., et al., Conscious Processing and the Global Neuronal Workspace Hypothesis. Neuron, 2020. 105(5): p. 776-798.
- 9. Mcmillan, W.L., Monte-Carlo Simulation of the Two-Dimensional Random (+/-J) Ising-Model. Physical Review B, 1983. 28(9): p. 5216-5220.
- 10. Clauset, A., C.R. Shalizi, and M.E.J. Newman, Power-Law Distributions in Empirical Data. Siam Review, 2009. 51(4): p. 661-703.
- 11. Beggs, J.M. and D. Plenz, Neuronal avalanches in neocortical circuits. Journal of Neuroscience, 2003. 23(35): p. 11167-11177.
- 12. Shew, W.L., et al., Neuronal Avalanches Imply Maximum Dynamic Range in Cortical Networks at Criticality. Journal of Neuroscience, 2009. 29(49): p. 15595-15600.
- 13. Zeng, G.X., et al., Short-term synaptic plasticity expands the operational range of long-term synaptic changes in neural networks. Neural Networks, 2019. 118: p. 140-147.
- 14. Poole, B., et al., Exponential expressivity in deep neural networks through transient chaos. Advances in Neural Information Processing Systems 29 (Nips 2016), 2016. 29.






