編輯:蛋醬、小舟
SVM is all you need,支持向量機永不過時。
Transformer 是一個支持向量機(SVM)一種新型理論在學界引發了人們的討論。
上周末,一篇來自賓夕法尼亞大學、加州大學河濱分校的論文試圖研究大模型基礎 Transformer 結構的原理,其在注意力層的優化幾何與將最優輸入 token 與非最優 token 分開的硬邊界 SVM 問題之間建立了形式等價。
在 hackernews 上作者表示,這種理論解決了 SVM 將每個輸入序列中的「好」標記與「壞」token 分開的問題。該 SVM 作為一個性能優異的 token 選擇器,與傳統為輸入分配 0-1 標簽的 SVM 本質上不同。
這種理論也解釋了注意力如何通過 softmax 引起稀疏性:落在 SVM 決策邊界錯誤一側的「壞」token 被 softmax 函數抑制,而「好」token 是那些最終具有非零 softmax 概率的 token。還值得一提的是,這個 SVM 源于 softmax 的指數性質。
論文上傳到 arXiv 上面之后,人們紛紛發表意見,有人表示:AI 研究的方向真是螺旋上升,難道又要繞回去了?
繞了一圈,支持向量機還是沒有過時。
自經典論文《Attention is All You Need》問世以來,Transformer 架構已為自然語言處理(NLP)領域帶來了革命性進展。Transformer 中的注意力層接受一系列輸入 token X,并通過計算
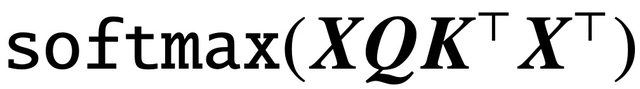
評估 token 之間的相關性,其中 (K, Q) 是可訓練的 key-query 參數,最終有效捕獲遠程依賴關系。
現在,一篇名為《Transformers as Support Vector machines》的新論文在自注意力的優化幾何和 hard-margin SVM 問題之間建立了一種形式等價,使用 token 對的外積線性約束將最優輸入 token 與非最優 token 分開。

論文鏈接:https://arxiv.org/pdf/2308.16898.pdf
這種形式等價建立在 Davoud Ataee Tarzanagh 等人的論文《Max-Margin Token Selection in Attention Mechanism》的基礎上,它能夠描述通過梯度下降進行優化的 1 層 transformer 的隱式偏差(implicit bias):
(1) 優化由 (K, Q) 參數化的注意力層,通過消失正則化(vanishing regularization),收斂到一種 SVM 解決方案,其中最小化組合參數
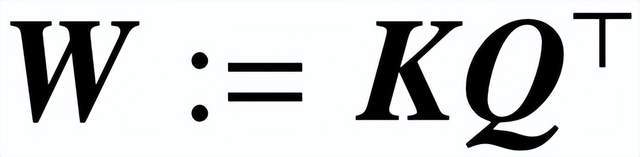
的核范數(nuclear norm)。相反,直接通過 W 進行參數化可以最小化 Frobenius 范數 SVM 目標。該論文描述了這種收斂,并強調它可以發生在局部最優方向而不是全局最優方向。
(2) 該論文還證明了 W 參數化在適當的幾何條件下梯度下降的局部 / 全局方向收斂。重要的是,過度參數化通過確保 SVM 問題的可行性和保證沒有駐點(stationary points)的良性優化環境來催化全局收斂。
(3) 雖然該研究的理論主要適用于線性預測頭,但研究團隊提出了一種更通用的 SVM 等價物,可以預測具有非線性頭 / MLP 的 1 層 transformer 的隱式偏差。
總的來說,該研究的結果適用于一般數據集,可以擴展到交叉注意力層,并且研究結論的實際有效性已經通過徹底的數值實驗得到了驗證。該研究建立一種新的研究視角,將多層 transformer 看作分離和選擇最佳 token 的 SVM 層次結構。
具體來說,給定長度為 T,嵌入維度為 d 的輸入序列
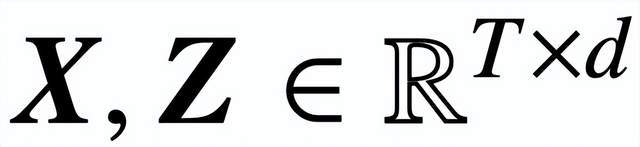
,該研究分析核心交叉注意力和自注意力模型:

其中,K、Q、V 分別是可訓練的鍵、查詢、值矩陣,
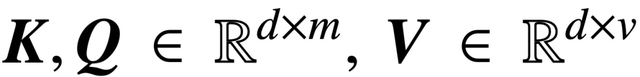
;S (?) 表示 softmax 非線性,它逐行應用于

。該研究假設將 Z 的第一個 token(用 z 表示)用于預測。具體來說,給定一個訓練數據集
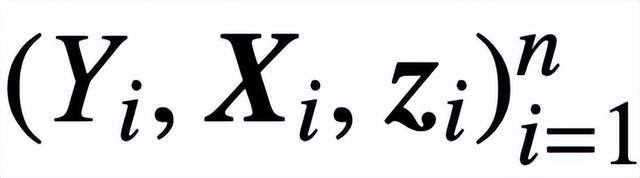
,
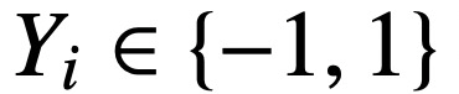
,
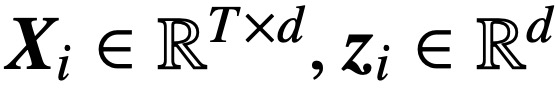
,該研究使用遞減損失函數

進行最小化:
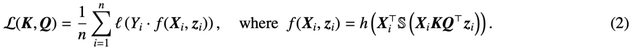
這里,h (?) :
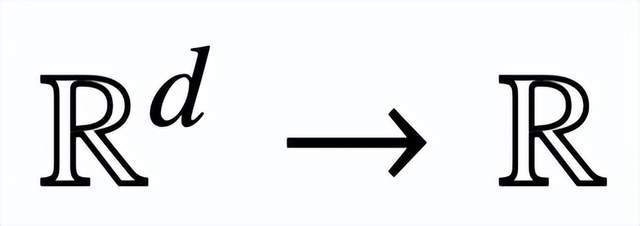
是包含值權重 V 的預測頭。在這種表述中,模型 f (?) 精確地表示了一個單層 transformer,其中注意力層之后是一個 MLP。作者通過設置
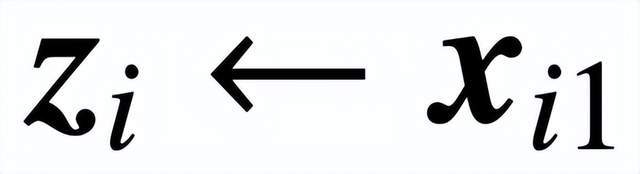
來恢復 (2) 中的自注意力,其中 x_i 表示序列 X_i 的第一個 token。由于 softmax 運算的非線性性質,它給優化帶來了巨大挑戰。即使預測頭是固定和線性的,該問題也是非凸和非線性的。在本研究中,作者將重點放在優化注意力權重(K、Q 或 W)上,并克服這些挑戰,從而建立 SVM 的基本等價性。
論文結構如下:第 2 章介紹了自注意力和優化的初步知識;第 3 章分析了自注意力的優化幾何,表明注意力參數 RP 收斂到最大邊際解;第 4 章和第 5 章分別介紹了全局和局部梯度下降分析,表明 key-query 變量 W 向 (Att-SVM) 的解決方案收斂;第 6 章提供了在非線性預測頭和廣義 SVM 等價性方面的結果;第 7 章將理論擴展到順序預測和因果預測;第 8 章討論了相關文獻。最后,第 9 章進行總結,提出開放性問題和未來研究方向。
論文的主要內容如下:
注意力層的內隱偏差(第 2-3 章)
正則化消失的情況下優化注意力參數(K, Q),會在方向上收斂到

的最大邊際解,其核范數目標是組合參數
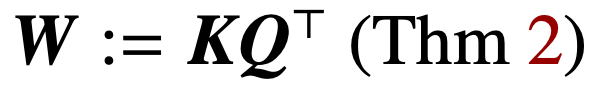
。在直接用組合參數 W 對交叉注意力進行參數化的情況下,正則化路徑 (RP) 定向收斂于以 Frobenius 范數為目標的(Att-SVM)解。
這是第一個正式區分 W 與(K,Q)參數化優化動態的結果,揭示了后者的低階偏差。該研究的理論清楚地描述了所選 token 的最優性,并自然地擴展到了序列到序列或因果分類設置。
梯度下降的收斂(第 4-5 章)
通過適當的初始化和線性頭 h (?),組合 key-query 變量 W 的梯度下降(GD)迭代在方向上收斂到(Att-SVM)的局部最優解(第 5 節)。要實現局部最優,所選 token 必須比相鄰 token 得分更高。
局部最優方向不一定是唯一的,可以根據問題的幾何特征來確定 [TLZO23]。作為一項重要貢獻,作者確定了保證向全局最優方向收斂的幾何條件(第 4 章)。這些條件包括:
- 最佳 token 在分數上有明顯區別;
- 初始梯度方向與最佳 token 一致。
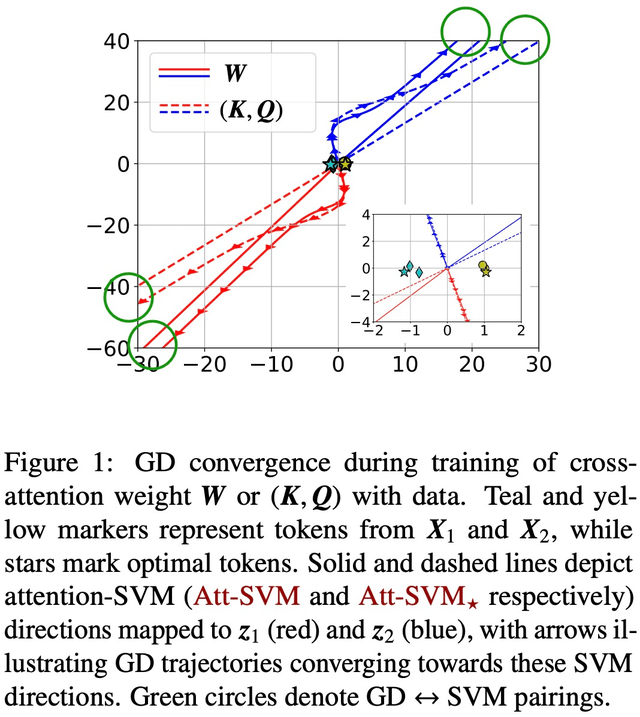
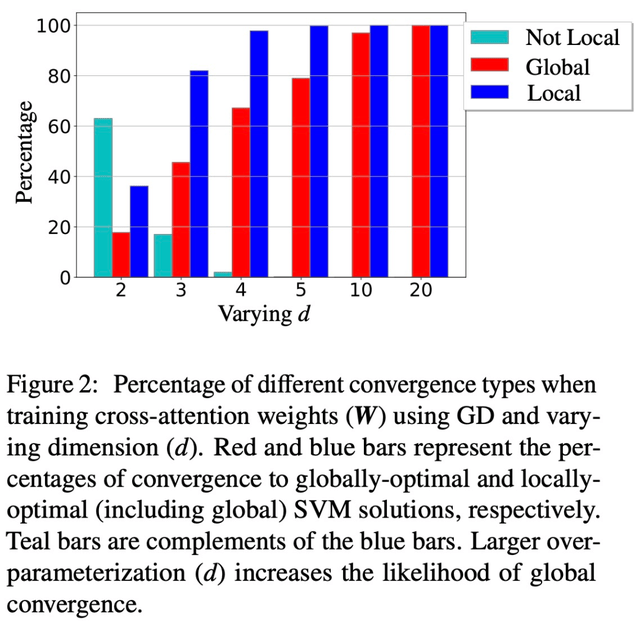
除此以外,論文還展示了過度參數化(即維度 d 較大,以及同等條件)通過確保(1)(Att-SVM)的可行性,以及(2)良性優化 landscape(即不存在靜止點和虛假的局部最優方向)來催化全局收斂(見第 5.2 節)。
圖 1 和圖 2 對此進行了說明。
SVM 等價的通用性(第 6 章)
當使用線性 h (?) 進行優化時,注意力層會固有地偏向于從每個序列中選擇一個 token(又稱硬注意力)。這反映在了 (Att-SVM) 中,表現為輸出 token 是輸入 token 的凸組合。與此相反,作者表明非線性頭必須由多個 token 組成,從而突出了它們在 transformer 動態過程中的重要性(第 6.1 節)。利用從理論中獲得的洞察力,作者提出了一種更通用的 SVM 等價方法。
值得注意的是,他們證明了在理論未涵蓋的普遍情況下(例如,h (?) 是一個 MLP),本文的方法能準確預測通過梯度下降訓練的注意力的隱含偏差。具體來說,本文的通用公式將注意力權重解耦為兩個部分:一個是由 SVM 控制的定向部分,它通過應用 0-1 掩碼來選擇標記;另一個是有限部分,它通過調整 softmax 概率來決定所選 token 的精確組成。
這些發現的一個重要特點是,它們適用于任意數據集(只要 SVM 可行),并且可以用數字驗證。作者通過實驗廣泛驗證了 transformer 的最大邊際等價性和隱含偏差。作者認為,這些發現有助于理解作為分層最大邊際 token 選擇機制的 transformer,可為即將開展的有關其優化和泛化動態的研究奠定基礎。
參考內容:
https://news.ycombinator.com/item?id=37367951
https://Twitter.com/vboykis/status/1698055632543207862






