01
一年級
第一單元 準備課
1、數一數
數數:數數時,按一定的順序數,從1開始,數到最后一個物體所對應的那個數,即最后數到幾,就是這種物體的總個數。
2、比多少
同樣多:當兩種物體一一對應后,都沒有剩余時,就說這兩種物體的數量同樣多。
比多少:當兩種物體一一對應后,其中一種物體有剩余,有剩余的那種物體多,沒有剩余的那種物體少。
比較兩種物體的多或少時,可以用一一對應的方法。
第二單元 位置
1、認識上、下
體會上、下的含義:從兩個物體的位置理解:上是指在高處的物體,下是指在低處的物體。
2、認識前、后
體會前、后的含義:一般指面對的方向就是前,背對的方向就是后。
同一物體,相對于不同的參照物,前后位置關系也會發生變化。
從而得出:確定兩個以上物體的前后位置關系時,要找準參照物,選擇的參照物不同,相對的前后位置關系也會發生變化。
3、 認識左、右
以自己的左手、右手所在的位置為標準,確定左邊和右邊。右手所在的一邊為右邊,左手所在的一邊為左邊。
要點提示:在確定左右時,除特殊要求,一般以觀察者的左右為準。
第三單元 1-5的認識和加減法
一、 1--5的認識
1、1—5各數的含義:每個數都可以表示不同物體的數量。有幾個物體就用幾來表示。
2、1—5各數的數序
從前往后數:1、2、3、4、5.
從后往前數:5、4、3、2、1.
3、1—5各數的寫法:根據每個數字的形狀,按數字在田字格中的位置,認真、工整地進行書寫。
二、比大小
1、前面的數等于后面的數,用“=”表示,即3=3,讀作3等于3。前面的數大于后面的數,用“>”表示,即3>2,讀作3大于2。前面的數小于后面的數,用“<”表示,即3<4,讀作3小于4。
2、填“>”或“<”時,開口對大數,尖角對小數。
三、第幾
1、確定物體的排列順序時,先確定數數的方向,然后從1開始點數,數到幾,它的順序就是“第幾”。第幾指的是其中的某一個。
2、區分“幾個”和“第幾”
“幾個”表示物體的多少,而“第幾”只表示其中的一個物體。
四、分與合
數的組成:一個數(1除外)分成幾和幾,先把這個數分成1和幾,依次分到幾和1為止。例如:5的組成有1和4,2和3,3和2,4和1.
把一個數分成幾和幾時,要有序地進行分解,防止重復或遺漏。
五、加法
1、加法的含義:把兩部分合在一起,求一共有多少,用加法計算。
2、加法的計算方法:計算5以內數的加法,可以采用點數、接著數、數的組成等方法。其中用數的組成計算是最常用的方法。
六、減法
1、減法的含義:從總數里去掉(減掉)一部分,求還剩多少用減法計算。
2、減法的計算方法:計算減法時,可以用倒著數、數的分成、想加算減的方法來計算。
七、0
1、0的意義:0表示一個物體也沒有,也表示起點。
2、0的讀法:0讀作:零
3、0的寫法:寫0時,要從上到下,從左到右,起筆處和收筆處要相連,并且要寫圓滑,不能有棱角。
4、0的加、減法:任何數與0相加都得這個數,任何數與0相減都得這個數,相同的兩個數相減等于0.
如:0+8=8 9-0=9 4-4=0
第四單元 認識圖形
1、長方體的特征:長長方方的,有6個平平的面,面有大有小。
如圖:
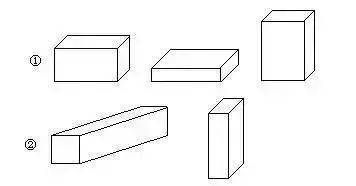
2、正方體的特征:四四方方的,有6個平平的面,面的大小一樣。
如圖:
3、圓柱的特征:直直的,上下一樣粗,上下兩個圓面大小一樣。放在桌子上能滾動。立在桌子上不能滾動。
如圖:

4、球的特征:圓圓的,很光滑,它的表面是曲面。放在桌子上能向任意方向滾動。
5、立體圖形的拼擺:用長方體或正方體能拼組出不同形狀的立體圖形,在拼好的立體圖形中,有一些部位從一個角度是看不到的,要從多個角度去觀察。用小圓柱可以拼成更大的圓柱。
02
二年級
第一單元 長度單位
1、常用的長度單位:米、厘米。
2、測量較短物體通常用厘米作單位,測量較長物體通常用米作單位。
3、測量物體長度的方法:將物體的左端對準直尺的“0”刻度,看物體的右端對著直尺上的刻度是幾,這個物體的長度就是幾厘米。
4、米和厘米的關系:1米=100厘米 100厘米=1米
5、線段
⑴線段的特點:①線段是直的;②線段有兩個端點;③線段有長有短,是可以量出長度的
⑵畫線段的方法:先用筆對準尺子的’0”刻度,在它的上面點一個點,再對準要畫到的長度的厘米刻度,在它的上面也點一個點,然后把這兩個點連起來,寫出線段的長度
⑶測量物體的長度時,當不是從“0”刻度量起時,要用終點的刻度數減去起點的刻度數。
6、填上合適的長度單位。
小明身高1(米)30(厘米)
練習本寬13(厘米)
鉛筆長17(厘米)
黑板長2(米)
圖釘長1(厘米)
一張床長2(米)
一口井深3(米)
學校進行100(米)賽跑
教學樓高25(米)
寶寶身高80(厘米)
跳繩長2(米)
一棵樹高3(米)
一把鑰匙長5(厘米)
一個文具盒長24(厘米)
講臺高90(厘米)
門高2(米)
教室長12(米)
筷子長20(厘米)
一棵小樹苗高1(米)
小朋友的頭圍48厘米
爸爸的身高1米75厘米或175厘米
小朋友的身高120厘米或1米20厘米
第二單元 100以內加減法
一、兩位數加兩位數
1、兩位數加兩位數不進位加法的計算法則:
把相同數位對齊列豎式,在把相同數位上的數相加。
2、兩位數加兩位數進位加法的計算法則:
①相同數位對齊;
②從個位加起;
③個位滿十向十位進1。
3、筆算兩位數加兩位數時,相同數位要對齊,從個位加起,個位滿十要向十位進“1”,十位上的數相加時,不要遺漏進上來的“1”。
4、和=加數+加數 一個加數=和-另一個加數
二、兩位數減兩位數
1、兩位數減兩位數不退位減的筆算:相同數位對齊列豎式,再把相同數位上的數相減。
2、兩位數減兩位數退位減的筆算法則:
①相同數位對齊;
②從個位減起;
③個位不夠減,從十位退1,在個位上加10再減。
3、筆算兩位數減兩位數時,相同數位要對齊,從個位減起,個位不夠減,從十位退1,個位加10再減,十位計算時要先減去退走的1再算。
4、差=被減數-減數
被減數=減數+差
減數=被減數-差
三、連加、連減和加減混合
1、連加、連連加、連減的筆算順序和連加、連減的口算順序一樣,都是從左往右依次計算。
①連加計算可以分步計算,也可以寫成一個豎式計算,計算方法與兩個數相加一樣,都要把相同數位對齊,從個位加起。
②連減運算可以分步計算,也可以寫成一個豎式計算,計算方法與兩個數相減一樣,都要把相同數位對齊,從個位減起。
2、加減混加、減混合算式,其運算順序、豎式寫法都與連加、連減相同。3、加減混合運算寫豎式時可以分步計算,方法與兩個數相加(減)一樣,要把相同數位對齊,從個位算起;也可以用簡便的寫法,列成一個豎式,先完成第一步計算,再用第一步的結果加(減)第二個數。
四、解決問題(應用題)
1、步驟:
①先讀題
②列橫式,寫結果,千萬別忘記寫單位(單位為:多少或者幾后面的那個字或詞)
③作答。
2、求“一個已知數”比“另一個已知數”多多少、少多少?用減法計算。用“比”字兩邊的較大數減去較小數。
3、比一個數多幾、少幾,求這個數的問題。先通過關鍵句分析,“比”字前面是大數還是小數,“比”字后面是大數還是小數,問題里面要求大數還是小數,求大數用加法,求小數用減法。
4、關于提問題的題目,可以這樣提問:
①…….和……一共…….?
②……比……..多多少/幾……?
③……比……..少多少/幾……?
第三單元 角的初步認識
1、角的初步認識
(1)角是由一個頂點和兩條邊組成的;
(2)畫角的方法:從一個點起,用尺子向不同的方向畫兩條直線。
(3)角的大小與邊的長短沒有關系,與角的兩條邊張開的大小有關,角的兩條邊張開得越大,角就越大,角的兩條邊張開得越小,角就越小。2、直角的初步認識
(1)直角的判斷方法:用三角尺上的直角比一比(頂點對頂點,一邊對一邊,再看另一條邊是否重合)。
(2)畫直角的方法:
①先畫一個頂點,再從這個點出發畫一條直線
②用三角尺上的直角頂點對齊這個點,一條直角邊對齊這條線
③再從這點出發沿著三角尺上的另一條直角邊畫一條線
④最后標出直角標志。
(3)比直角小的是銳角,比直角大的是鈍角:銳角<直角<鈍角。
(4)所有的直角都一樣大
(5)每個三角尺上都有1個直角,兩個銳角。紅領巾上有3個角,其中一個是鈍角,兩個是銳角。一個長方形中和正方形中都是有4個直角。
第四、六單元 表內乘法(一)(二)
1、乘法的含義
乘法是求幾個相同加數連加的和的簡便算法。如:計算:2+2+2=6,用乘法算就是:2×3=6或3×2=6.
2、乘法算式的寫法和讀法
⑴連加算式改寫為乘法算式的方法。求幾個相同加數的和,可以用乘法計算。寫乘法算式時,可以用乘法計算。寫乘法算式時,可以先寫相同的加數,然后寫乘號,再寫相同加數的個數,最后寫等號與連加的和;也可以先寫相同加數的個數,然后寫乘號,再寫相同加數,最后寫等號與連加的和。
如:4+4+4=12改寫成乘法算式是4×3=12或3×4=12
⑵乘法算式的讀法。讀乘法算式時,要按照算式順序來讀。如:6×3=18讀作:“6乘3等于18”。
3、乘法算式中各部分的名稱及實際表示的意義
在乘法算式里,乘號前面的數和乘號后面的數都叫做“乘數”;等號后面的得數叫做“積”。
4、乘法算式所表示的意
求幾個相同加數的和,用乘法計算比較簡單。一道乘法算式表示的就是幾個相同加數連加的和。如:
4×5表示5個4相加或4個5相加。
5、加法寫成乘法時,加法的和與乘法的積相同。
6、乘法算式中,兩個乘數交換位置,積不變。
7、算式各部分名稱及計算公式。
乘法:乘數×乘數=積
加法:加數+加數=和
和—加數=加數
減法:被減數—減數=差
被減數=差+減數
減數=被減數—差
8、在9的乘法口訣里,幾乘9或9乘幾,都可看作幾十減幾,其中“幾”是指相同的數。
如:1×9=10—1 9×5=50—5
9、看圖,寫乘加、乘減算式時:
乘加:先把相同的部分用乘法表示,再加上不相同的部分。
乘減:先把每一份都算成相同的,寫成乘法,然后再把多算進去的減去。
計算時,先算乘,再算加減。
如:加法:3+3+3+3+2=14
乘加:3×4+2=14
乘減:3×5-1=14
10、“幾和幾相加”與“幾個幾相加”有區別求幾和幾相加,用幾加幾;
如:求4和3相加是多少?
用加法(4+3=7)求幾個幾相加,用幾乘幾。
如:求4個3相加是多少?(3+3+3+3=12或3×4=12或4×3=12)
補充:幾和幾相乘,求積?用幾×幾。
如:2和4相乘用2×4=82個
乘數都是幾,求積?用幾×幾。
如:2個8相乘用8×8=6411、
一個乘法算式可以表示兩個意義,
如“4×2”既可以表示“4個2相加”,也可以表示“2個4相加”。
“5+5+5”寫成乘法算式是(3×5=15)或(5×3=15),都可以用口訣(三五十五)來計算,表示(3)個(5)相加3×5=15讀作:3乘5等于15。5×3=15讀作:5乘3等于15
03
三年級
第一單元 時、分、秒
1、鐘面上有3根針,它們是(時針)、(分針)、(秒針),其中走得最快的是(秒針),走得最慢的是(時針)。(時針最短,秒針最長)
2、鐘面上有(12)個數字,(12)個大格,(60)個小格;每兩個數間是(1)個大格,也就是(5)個小格。
3、時針走1大格是(1)小時;分針走1大格是(5)分鐘,走1小格是( 1)分鐘;秒針走1大格是(5)秒鐘,走1小格是(1)秒鐘。
4、時針走1大格,分針正好走(1)圈,分針走1圈是(60)分,也就是(1)小時。時針走1圈,分針要走(12)圈。
5、分針走1小格,秒針正好走(1)圈,秒針走1圈是(60)秒,也就是(1)分鐘。
6、時針從一個數走到下一個數是(1小時)。分針從一個數走到下一個數是(5分鐘)。秒針從一個數走到下一個數是(5秒鐘)。
7、公式。(每兩個相鄰的時間單位之間的進率是60)
1時=60分 1分=60秒 60分=1時 60秒=1分
第二、四單元 萬以內的加法和減法
1、認識整千數(記憶:10個一千是一萬)
2、讀數和寫數(讀數時寫漢字 寫數時寫阿拉伯數字)
①一個數的末尾不管有一個0或幾個0,這個0都不讀。
②一個數的中間有一個0或連續的兩個0,都只讀一個0。
3、數的大小比較:
①位數不同的數比較大小,位數多的數大。
②位數相同的數比較大小,先比較這兩個數的最高位上的數,如果最高位上的數相同,就比較下一位,以此類推。
4、求一個數的近似數:
記憶:看最位的后面一位,如果是0-4則用四舍法,如果是5-9就用五入法。
5、最大的幾位數和最小的幾位數
最大的一位數是9,最小的一位數是0.
最大的二位數是99,最小的二位數是10
最大的三位數是999,最小的三位數是100
最大的四位數是9999,最小的四位數是1000
最大的三位數比最小的四位數小1。
6、被減數是三位數的連續退位減法的運算步驟:
① 列豎式時相同數位一定要對齊;
② 減法時,哪一位上的數不夠減,從前一位退1,在本位上加上10再減;如果前一位是0,則再從前一位退1。
7、兩個三位數相加的和:可能是三位數,也有可能是四位數。
8、公式:被減數=減數+差
和=加數+另一個加數
減數=被減數-差
加數=和-另一個加數
差=被減數-減數
第三單元 測量
1、在生活中,量比較短的物品,可以用(毫米、厘米、分米)做單位;量比較長的物體,常用(米)做單位;測量比較長的路程一般用(千米)做單位,千米也叫(公里)。
2、1厘米的長度里有(10)小格,每小格的長度(相等),都是(1)毫米。
3、1枚1分的硬幣、尺子、磁卡、小紐扣、鑰匙的厚度大約是1毫米。
4、在計算長度時,只有相同的長度單位才能相加減。
5、長度單位的關系式有:( 每兩個相鄰的長度單位之間的進率是10 )
① 進率是10:1米=10分米,
1分米=10厘米, 1厘米=10毫米,
② 進率是100:
1米=100厘米, 1分米=100毫米,
③ 進率是1000:1千米=1000米,
6、當我們表示物體有多重時,通常要用到(質量單位)。在生活中,稱比較輕的物品的質量,可以用( 克 )做單位;稱一般物品的質量,常用(千克 )做單位;計量較重的或大宗物品的質量,通常用( 噸 )做單位。
小技巧:在“噸”與“千克”的換算中,把噸換算成千克,是在數字的末尾加上3個0; 把千克換算成噸,是在數字的末尾去掉3個0。
7、相鄰兩個質量單位進率是1000。
1噸=1000千克 1千克=1000克
1000千克= 1噸 1000克=1千克
04
四年級
第一單元 大數的認識
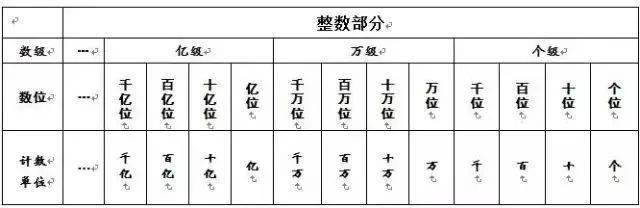
1.10個一萬是十萬,10個十萬是一百萬,10個一百萬是一千萬,10個一千萬是一億。
相鄰兩個計數單位之間的進率是“十” ,這種計數方法叫做十進制計數法。
特別注意:計數單位與數位的區別。
2、在用數字表示數的時候,這些計數單位要按照一定的順序排列起來,它們所占的位置叫做數位。
3、位數:一個數含有幾個數位,就是幾位數,如652100是個六位數。
4、按照我國的計數習慣,從右邊起,每四個數位是一級。
6、億以上數的讀法:
① 先分級,從高位開始讀起。先讀億級,再讀萬級,最后讀個級。
② 億級的數要按照個級的數的讀法來讀,再在后面加上一個“億”字。萬級的數要按照個級的數的讀法來讀,再在后面加上一個“萬”字。
③ 每級末尾不管有幾個0,都不讀。其他數位有一個“0”或連續幾個“0”,都只讀一個“0”。
7、億以上數的寫法:
① 從最高位寫起,先寫億級,再寫萬級,最后寫個級。
② 哪個數位上一個單位也沒有,就在那個數位上寫0。
8、比較數的大小:
① 位數不同的兩個數,位數多的數比較大。
② 位數相同的兩個數,從最高位開始比較。
9、求近似數:
省略萬位后面的尾數,要看千位上的數;省略億位后面的尾數,要看千萬位上的數。
這種求近似數的方法叫“四舍五入法”,是“舍”還是“入”,要看省略的尾數最高位上的數是小于5 還是等于或大于5 。小于5就舍去尾數,等于或大于5就向前一位進1,再舍去尾數。
10、表示物體個數:1,2 ,3, 4, 5 ,6 ,7 ,8 ,9 ,10, ……. 都是自然數。一個物體也沒有,用0來表示, 0也是自然數。所有的自然數都是整數。
11、最小的自然數是0,沒有最大的自然數,自然數的個數是無限的。
12、每相鄰的兩個計數單位之間的進率都是十,這種計數方法叫做十進制計數法。
第二單元 公頃和平方千米
1、邊長是100米的正方形面積是1公頃。
1公頃 = 10000平方米
2、邊長是1千米的正方形面積是1平方千米。
1平方千米 = 1000000平方米
1平方千米=100公頃
3、從大單位變到小單位,乘以進率。
從小單位變到大單位,除以進率。
4、國土面積(中國、省、市、區等)、海洋面積等特別大的面積適合用平方千米。如:香港特別行政區的面積約1100(平方千米)。
廣場、校園等稍大土地面積適合用公頃。如天安門廣場的占地面積大約是44(公頃);
操場、教室等較小的面積適合用平方米。如一個教室的面積約60(平方米);
5、長方形面積 = 長 × 寬
正方形面積 = 邊長 × 邊長
第三單元 角的度量
1、直線、射線、線段
直線:可以向兩端無限延伸,沒有端點。
射線:可以向一端無限延伸,只有一個端點。
線段:不能延伸,有兩個端點,線段是直線的一部分。
2、直線、射線與線段有什么聯系和區別?
①直線和射線都可以無限延伸,因此無法量出長短。
②線段可以量出長度。
3.從一點引出兩條射線所組成的圖形叫做角。
4、角的計量單位是“度”,用符號“ °”表示。
將圓平均分成360 份,每一份所對的角的大小是l 度,記做1°。
5、角的大小與角兩邊的長短沒關系。角的大小與叉開的大小有關系,叉開得越大,角越大。
6、度量角的工具叫量角器。
7、量角的步驟:
①把量角器的中心與角的頂點重合,0°刻度線與角的一條邊重合。
②角的另一條邊所對的量角器上的刻度,就是這個角的度數。
8、角可以看作由一條射線繞著它的端點,從一個位置旋轉到另一個位置所成的圖形。
9、一條射線繞它的端點旋轉半周,形成的角叫做平角。1平角=180°
10、一條射線繞它的端點旋轉一周,形成的角叫做周角。1周角=360°
1周角=2平角=4直角 1直角=90°
11、小于90度的角叫做銳角,大于90度而小于180度的角叫做鈍角。
銳角<直角<鈍角<平角<周角
12、畫角的步驟:
(1)畫一條射線,使量角器的中心和射線的端點重合,0°刻度線和射線重合。
(2)在量角器上找到要畫的角的度數(如65°)的地方,并點一個點。
(3)以畫出的射線的端點為端點,通過剛畫的點再畫一條射線。
13、經過一點可以畫無數條直線;經過兩個點,只能畫一條直線。
14、用三角板可以畫的角:
180°165°150°135°120°105°90°75°60°45°30°15°
第四單元 三位數乘兩位數
1、三位數乘兩位數的筆算方法:
先用兩位數個位上的數去乘三位數,積的末位和兩位數的個位對齊;再用兩位數十位上的數去乘三位數,積的末位和兩位數的十位對齊;最后把兩次乘得的積加起來。
2、積的變化規律:
一個因數不變,另一個因數乘(或除以)幾(0除外),積也乘(或除以)幾。
3、每件商品的價錢,叫做單價;買了多少,叫做數量;一共用的價錢,叫做總價。
單價 ×數量 = 總價
單價=總價 ÷ 數量
4、一共行了多長的路,叫做路程;每小時(或每分鐘等)行的路程,叫做速度;行了幾小時(或幾分鐘等),叫做時間。
速度 ×時間= 路程
速度=路程 ÷ 時間
時間=路程 ÷ 速度
5、速度單位通常有:千米/時、米/分、米/秒等。
05
五年級
第一單元 小數乘法
1、小數乘法的計算方法:先把小數擴大成整數;按整數乘法的法則算出積;再看因數中一共有幾位小數,就從積的右邊起數出幾位點上小數點。乘得的積小數位數不夠時,就在積的前面用0來補足,再點小數點。
2、計算結果中,小數部分末尾的0要去掉,把小數化簡。
3、規律:一個數(0除外)乘大于1的數,積比原來的數大。一個數(0除外)乘小于1的數,積比原來的數小。一個數(0除外)乘1,積等于原來的數。
4、求近似數的方法有三種:⑴四舍五入法;⑵進一法;⑶去尾法。
5、計算錢數,保留兩位小數,表示計算到分。保留一位小數,表示計算到角。
6、小數四則運算順序跟整數是一樣的。乘法交換律、乘法結合律、乘法分配律對于小數乘法同樣適用。
7、運算定律和性質加法:加法交換律:a+b=b+a加法結合律:(a+b)+c=a+(b+c)減法:減法性質:a-b-c=a-(b+c)a-(b-c)=a-b+c乘法:乘法交換律:a×b=b×a乘法結合律:(a×b)×c=a×(b×c)乘法分配律:(a+b)×c=a×c+b×c或(a-b)×c=a×c-b×c除法:除法性質:a÷b÷c=a÷(b×c)
第二單元 位置
1、用數對表示位置時,一般列數在前面,行數在后面。
第三單元 小數除法
1、小數除以整數的計算方法:小數除以整數,按整數除法的方法去除。商的小數點要和被除數的小數點對齊。整數部分不夠除,商0,點上小數點。如果有余數,要添0再除。
2、小數除以小數的計算方法:先將除數和被除數擴大相同的倍數,使除數變成整數,再按“小數除以整數的計算方法”進行計算。
3、如果被除數的位數不夠,在被除數的末尾用0補足。
4、在實際應用中,小數除法所得的商也可以根據需要用“四舍五入”法保留一定的小數位數,求出商的近似數。求商的近似數時,近似數的末尾的0不能去掉。
5、除法中的變化規律:
(1)商不變:被除數和除數同時擴大或縮小相同的倍數(0除外),商不變。
(2)除數不變:被除數擴大,商隨著擴大。
(3)被除數不變:除數縮小,商擴大。
6、循環小數:一個數的小數部分,從某一位起,一個數字或者幾個數字依次不斷重復出現,這樣的小數叫做循環小數。
7、一個循環小數的小數部分,依次不斷重復出現的數字,叫做循環節。
8、小數部分的位數是有限的小數,叫做有限小數。小數部分的位數是無限的小數,叫做無限小數。
第四單元 可能性
1. 可能性
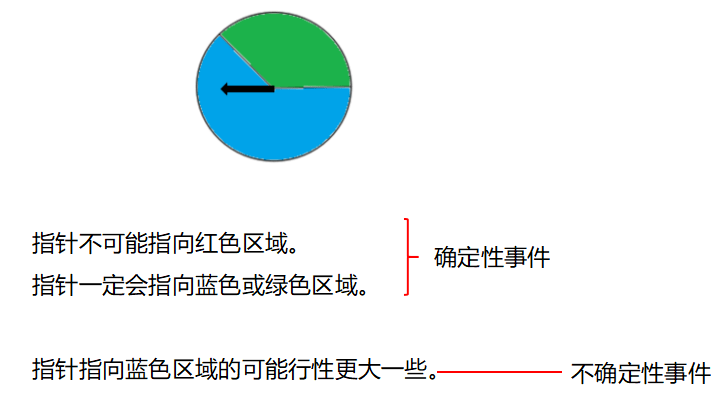
事件的發生有確定性和不確定性,確定的事件用“一定”或“不可能”來描述,不確定的事件用“可能”來描述。
2. 事件發生可能性的大小
可能性的大小與數量的多少有關,相同條件下,在總數中所占數量越多,可能性越大;所占數量越少,可能性越小。
06
六年級
第一單元 分數乘法
(一)分數乘法意義:
1、分數乘整數的意義與整數乘法的意義相同,就是求幾個相同加數的和的簡便運算。
“分數乘整數”指的是第二個因數必須是整數,不能是分數。
2、一個數乘分數的意義就是求一個數的幾分之幾是多少。
“一個數乘分數”指的是第二個因數必須是分數,不能是整數。(第一個因數是什么都可以)
(二)分數乘法計算法則:
1、分數乘整數的運算法則是:分子與整數相乘,分母不變。
(1)為了計算簡便能約分的可先約分再計算。(整數和分母約分)
(2)約分是用整數和下面的分母約掉最大公因數。(整數千萬不能與分母相乘,計算結果必須是最簡分數)。
2、分數乘分數的運算法則是:用分子相乘的積做分子,分母相乘的積做分母。(分子乘分子,分母乘分母)
(1)如果分數乘法算式中含有帶分數,要先把帶分數化成假分數再計算。
(2)分數化簡的方法是:分子、分母同時除以它們的最大公因數。
(3)在乘的過程中約分,是把分子、分母中,兩個可以約分的數先劃去,再分別在它們的上、下方寫出約分后的數。(約分后分子和分母必須不再含有公因數,這樣計算后的結果才是最簡單分數)。
(4)分數的基本性質:分子、分母同時乘或者除以一個相同的數(0除外),分數的大小不變。
(三)積與因數的關系:
一個數(0除外)乘大于1的數,積大于這個數。a×b=c,當b>1時,c>a。
一個數(0除外)乘小于1的數,積小于這個數。a×b=c,當b<1時,c<a(b≠0)。
一個數(0除外)乘等于1的數,積等于這個數。a×b=c,當b=1時,c=a。
在進行因數與積的大小比較時,要注意因數為0時的特殊情況。
(四)分數乘法混合運算
1、分數乘法混合運算順序與整數相同,先乘、除后加、減,有括號的先算括號里面的,再算括號外面的。
2、整數乘法運算定律對分數乘法同樣適用;運算定律可以使一些計算簡便。
乘法交換律:a×b=b×a
乘法結合律:(a×b)×c=a×(b×c)
乘法分配律:a×(b±c)=a×b±a×c
(五)倒數的意義:乘積為1的兩個數互為倒數。
1、倒數是兩個數的關系,它們互相依存,不能單獨存在。單獨一個數不能稱為倒數。(必須說清誰是誰的倒數)
2、判斷兩個數是否互為倒數的唯一標準是:兩數相乘的積是否為“1”。例如:a×b=1,則a、b互為倒數。
3、求倒數的方法:
①求分數的倒數:交換分子、分母的位置。
②求整數的倒數:整數分之1。
③求帶分數的倒數:先化成假分數,再求倒數。
④求小數的倒數:先化成分數再求倒數。
4、1的倒數是它本身,因為1×1=1。
0沒有倒數,因為任何數乘0積都是0,且0不能作分母。
5、真分數的倒數是假分數,真分數的倒數大于1,也大于它本身。
假分數的倒數小于或等于1。帶分數的倒數小于1。
(六)分數乘法應用題——用分數乘法解決問題
1、求一個數的幾分之幾是多少?(用乘法)
已知單位“1”的量,求單位“1”的量的幾分之幾是多少,用單位“1”的量與分數相乘。
2、巧找單位“1”的量:在含有分數(分率)的語句中,分率前面的量就是單位“1”對應的量,或者“占”“是”“比”字后面的量是單位“1”。
3、什么是速度?
速度是單位時間內行駛的路程。
速度=路程÷時間
時間=路程÷速度
路程=速度×時間
單位時間指的是1小時1分鐘1秒等這樣的大小為1的時間單位,每分鐘、每小時、每秒鐘等。
4、求甲比乙多(少)幾分之幾?
多:(甲-乙)÷乙
少:(乙-甲)÷乙
第二單元 位置與方向(二)
1、什么是數對?
數對:由兩個數組成,中間用逗號隔開,用括號括起來。括號里面的數由左至右為列數和行數,即“先列后行”。
數對的作用:確定一個點的位置。經度和緯度就是這個原理。
2、確定物體位置的方法:
(1)先找觀測點;(2)再定方向(看方向夾角的度數);(3)最后確定距離(看比例尺)。
描繪路線圖的關鍵是選好觀測點,建立方向標,確定方向和路程。
位置關系的相對性:兩地的位置具有相對性在敘述兩地的位置關系時,觀測點不同,敘述的方向正好相反,而度數和距離正好相等。
相對位置:東-西;南-北;南偏東-北偏西。
第三單元 分數的除法
一、分數除法的意義:分數除法是分數乘法的逆運算,已知兩個數的積與其中一個因數,求另一個因數的運算。
二、分數除法計算法則:除以一個數(0除外),等于乘上這個數的倒數。
1、被除數÷除數=被除數×除數的倒數。
2、除法轉化成乘法時,被除數一定不能變,“÷”變成“×”,除數變成它的倒數。
3、分數除法算式中出現小數、帶分數時要先化成分數、假分數再計算。
4、被除數與商的變化規律:
①除以大于1的數,商小于被除數:a÷b=c,當b>1時,c<a。
②除以小于1的數,商大于被除數:a÷b=c,當b<1時,c>a。(a≠0,b≠0)
③除以等于1的數,商等于被除數:a÷b=c,當b=1時,c=a。
三、分數除法混合運算
1、混合運算用梯等式計算,等號寫在第一個數字的左下角。
2、運算順序:
①連除:同級運算,按照從左往右的順序進行計算;或者先把所有除法轉化成乘法再計算;或者依據“除以幾個數,等于乘上這幾個數的積”的簡便方法計算。加、減法為一級運算,乘、除法為二級運算。
②混合運算:沒有括號的先乘、除后加、減,有括號的先算括號里面,再算括號外面。
(a±b)÷c=a÷c±b÷c
第四單元 比
比:兩個數相除也叫兩個數的比
1、比式中,比號(∶)前面的數叫前項,比號后面的項叫做后項,比號相當于除號,比的前項除以后項的商叫做比值。
連比,如:3:4:5讀作:3比4比5。
2、比表示的是兩個數的關系,可以用分數表示,寫成分數的形式,讀作幾比幾。
例:12∶20=12÷20=0.6
12∶20讀作:12比20。
區分比和比值:比值是一個數,通常用分數表示,也可以是整數、小數。
比是一個式子,表示兩個數的關系,可以寫成比,也可以寫成分數的形式。
3、比的基本性質:比的前項和后項同時乘以或除以相同的數(0除外),比值不變。
4、化簡比:化簡之后結果還是一個比,不是一個數。
(1)用比的前項和后項同時除以它們的最大公約數。
(2)兩個分數的比,用前項后項同時乘分母的最小公倍數,再按化簡整數比的方法來化簡。也可以求出比值再寫成比的形式。
(3)兩個小數的比,向右移動小數點的位置,也是先化成整數比。
5、求比值:把比號寫成除號再計算,結果是一個數(或分數),相當于商,不是比。
6、比和除法、分數的區別:
除法:被除數除號(÷) 除數(不能為0) 商不變性質 除法是一種運算。
分數:分子分數線(—)分母(不能為0) 分數的基本性質 分數是一個數。
比:前項比號(∶) 后項(不能為0) 比的基本性質 比表示兩個數的關系。
商不變性質:被除數和除數同時乘或除以相同的數(0除外),商不變。
分數的基本性質:分子和分母同時乘或除以相同的數(0除外),分數的大小不變。
分數除法和比的應用
1、已知單位“1”的量用乘法。
2、未知單位“1”的量用除法。
3、分數應用題基本數量關系(把分數看成比)
(1)甲是乙的幾分之幾?
甲=乙×幾分之幾
乙=甲÷幾分之幾
幾分之幾=甲÷乙
(2)甲比乙多(少)幾分之幾?
4、按比例分配:把一個量按一定的比分配的方法叫做按比例分配。
5、畫線段圖:
(1)找出單位“1”的量,先畫出單位“1”,標出已知和未知。
(2)分析數量關系。
(3)找等量關系。
(4)列方程。
兩個量的關系畫兩條線段圖,部分和整體的關系畫一條線段圖。






